On ray casting, ray tracing, ray marching and the like
Introduction
There is a hype especially about ray marching in the demoscene. This is what people call a technique that is used mostly in 4k procedural graphics and 4k intros to create 3d pictures with interesting looks. Since there used to be no comprehensive tutorial on the matter, many people initially found it confusing to understand the underlying principle, which we can see in the huge number of threads in the pouet.net BBS dealing with various aspects of ray marching. The answers more experienced coders gave were partially a bit hard to grasp, and so I guess there are still some people around who do not really feel satisfied with their understanding of ray casting, ray tracing, ray marching and the like. For these people, I've written the following article.
History: It's all about 3d
While the first scrollers were strictly two-dimensional, 3d effects became omnipresent in demos rather soon. Already in C64 demos of the 1980s we can spot things such as rotating cubes. While first only the lines of the cubes were displayed, it did not take long until techniques to fill the sides with colours emerged: flat shading, gouraud shading, phong shading - you name them.
Cubes were followed by more complex objects such as dodecahedra. To display spheres, a technique known as tessellation was used: the round surface was subdivided into a lot of small polygons; thus the shape of the sphere was approximated.
Techniques such as ray marching are a different way of displaying 3d objects. Since they are computationally more expensive, they were not often used in demos until computers became more powerful; you might remember the 64k intro Heaven Seven by Exceed from 1999, which featured realtime ray tracing. The demoscene, however, would not be the demoscene if it did not try to break barriers, and by now you can also find some sorts of ray casting in productions made for weaker systems.
Terminology
Ray casting, ray tracing, ray marching - are they different things, or are they just different names for the same thing or similar things? The latter possibility applies. As a matter of fact the original method is ray casting, and the other two are just variants of it. Ray tracing is a more sophisticated algorithm involving diffraction and reflection, thus generating images looking even more realistic; alas, it is computationally more expensive, of course. Ray marching, which is the thing that is so popular in the demoscene at the moment, is a variant of ray casting that permits the use of objects for which there is no analytic formula so that the intersection with the ray cannot be simply computed by solving an algebraic equation. Ray marching is also called sphere tracing, for a reason I will explain later on. Actually what's most widely used in the demoscene is not the general ray marching algorithm, but a variant of it involving a distance field - I'll show you what this is all about. Of course ray marching and ray tracing techniques can be combined (and that's just what's done in the demoscene), the two terms are not mutually exclusive.
General Ray casting
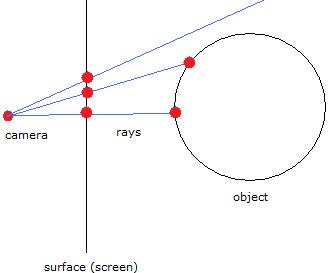
In general, ray casting is about displaying a 3d scene involving one or several objects. The basic idea is: You have a camera (you may also call it viewport, or the human eye) that looks at a surface (the screen). The objects are located behind this surface and are projected on it. What ray casting is all about is to determine the colour of each pixel on the screen. Imagine that you send out rays from your eye, which pass through the surface. Each pixel can be accessed by one ray. If you continue following the ray behind the surface, it will sooner or later hit one of the objects in the scene. This is the object you see at that pixel. In the most basic variant of ray casting, the colour of the pixel is simply a function of the distance from the camera to the point where the ray hits the object (the intersection point). So the ray casting algorithm has to calculate the intersection points of all the rays with all the objects, pick the closest intersection point and calculate the distance to the camera.

How to compute the intersection points?
To compute the intersection point of a ray with an object, you need the formulas of both the ray and the object surface.
A ray is a straight line. Lines can be mathematically represented in various ways, one of them being the vector form:
P = A + t * (B - A)
That means: Any point P is the sum of the coordinates of a point A plus the product of a vector AB and a scalar t.
We get the intersection point of a ray with an object by inserting the formulas for x, y and z into the formula that describes the object and solving for t. E.g. for a sphere:
|P - C| = r
Here C is the center point.
Inserting this we get:
|A + t * (B - A) - C| = r
(A - C)^2 + 2 * t * (A - C) * (B - A) + t^2 * (B - A)^2 = r^2
By inserting the coordinates of A, B and C and solving for t (quadratic equation, solvable using the standard formula for quadratic equations) we can compute the coordinates of P.
So that's how traditional ray casting works. How about ray marching?
Ray marching
The ray marching algorithm has the advantage over traditional ray casting that you need not compute intersection points analytically. Instead, you walk along the ray and simply check after each step whether you've hit an object.
The distance you walk per step may be constant or variable. In the simpler, constant case, the easiest way is to take the vector P1P2 (where P1 is the location of the camera and P2 the surface point the colour of which you want to compute) and add it to the current point at each step, starting with P2. So you need not even compute an analytic function of the ray. All you do is calculate the x, y, z coordinates for the current point and insert it into the formulas of the objects. Now if some point Pa has coordinates for which the sphere equation results in the left side being lower than the right side, and the next point Pa+1 yields the opposite result (the left side is greater than the right side), you know that somewhere between Pa and Pa+1, the sphere has been hit. By keeping track of the number of steps you have walked on the ray, you have automatically obtained the distance, and thus are able to calculate the colour of the pixel to put.
This approach is far easier to implement than standard ray casting. It may be a bit slow if the distance you walk on the rays is low and the objects are far away, but that does not seem to matter much. A real disadvantage is that it is not precise and depends on the distance you walk per step. The larger the distance per step, the faster it goes, but the less accurate it is. Large distances per steps also have the disadvantage that you might overlook objects as it may be possible that they are so small that you virtually step over them, and do not notice that the ray has hit them between two subsequent points. (You can only detect an object if one point is outside of it, and the next point inside. If both points are outside, then you will not notice anything.) So the distance per step is a crucial point.
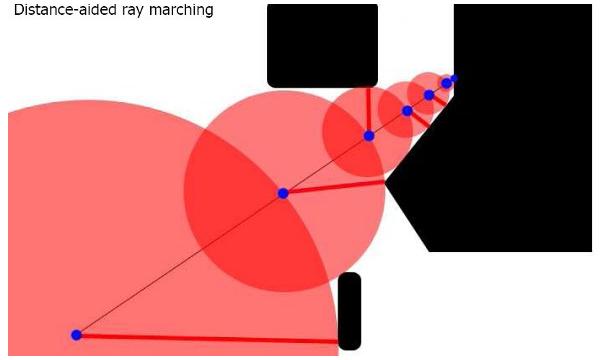
Distance-aided ray marching
What is especially popular in the demoscene at the moment is distance-aided ray marching. The basic idea is that the distance per step is not constant, but variable. It depends on the distance of the current point to the object that is closest to it. If you know that distance, it is safe to walk exactly that distance on the ray, as chances are zero that you will hit an object if you walk less than that.
The distance to an object can be computed far more easily than the distance between a point and the intersection of a ray starting at that point with an object. For example, if the object is a sphere you only have to compute the length of the vector from the point to the center, and subtract the radius from it.
Other applications of ray marching
Ray marching also has the advantage over traditional ray casting that you need not have analytic formulas of the objects in the 3d scene. You may also use it with volumetric data, like a set of voxels. This is the technique that is used in 3d reconstruction of CT scans in clinical radiology, for instance.
Sphere tracing
The reason why ray marching is sometimes also called sphere tracing: You can picture the distance between two steps as the radius of a sphere. Each of these spheres touches at least one object. So you virtually follow the intersection points of these spheres with the ray.
Ray tracing
A couple of words on ray tracing: The main idea behind that is that you do not only compute the ray from the camera to the object, but also from the object to the light source, whereever it is. By checking whether an object actually gets light and taking this into consideration in the formula computing the colour of the pixel, you can get more realistic pictures. Moreover, reflection and diffraction can be implemented as well, to make the pictures looking even more like photos.
Conclusion
This article has been the most demoscene-related of the technical articles I've written so far, and I hope that it has fulfilled its purpose.
Links related to this article
The original paper about sphere tracing (page not available?)
Rendering Worlds with Two Triangles - presentation by iq/rgba
A paper about Ray tracing implicit surfaces on the GPU
An unfinished draft of a tutorial on distance fields and sphere tracing
A paper on Generalized Distance Functions
Wikipedia on Ray casting
Wikipedia on Ray tracing
Wikipedia on Distance fields
Pouet.net: Raymarching Beginners' Thread
Pouet.net: Raymarching Toolbox Thread
Pouet.net: Thread about distance field equations
Pouet.net: Problem with ray marching when applying twist distortion
Pouet.net: Raymarching idea - Invertible Surfaces
Pouet.net: Thread about the making of Cdak by Quite
Pouet.net: Trick for 1k raymarchers - lighting
Pouet.net: Implicit function to distance function
Example: Terrain Ray Marching in Processing
Example: 704 (1k JavaScript intro involving ray marching)
Example: Valleyball by BluFlame
Example: Legoland 2 by Fairlight (ray tracing on C64)
Example: Slisesix by Rgba
Example: Fallty by Loonies (one of the first intros using ray marching)
Example: Puls by Rrrola (256b intro using ray marching)
Example: Cdak by Quite and Orange
Example: nop by Stroboholics and Metalvotze