A 3D Iterated function system fractal editor
By Seven/Fulcrum
Iterated function systems or IFS fractals have been used in many demos, Verses/EMF is one of the first I remember, and Animal Attraction/ASD one of the most recent (in the "zooming out of recursive boxes"-part, the paintings on the walls have animated IFS fractals). Most demos use 2D IFS fractals only, a couple also have 3D fractals. However, most of the 3D fractals are either randomly generated, or well-known examples such as the fern, trees or a Sierpinski pyramid or cube. My guess is that while there are many free tools to make 2D IFS fractals (FractInt etc), there doesn't seem to be any for 3D fractals. So I decided to make my own tool, to make more "interesting" fractals to use in a demo.
The editor has gone through several unfinished iterations over a couple of years, but last year I finally got the time and the drive to finish the tool and make a demo with it (called Heliosphere, placed 2nd at Buenzli06). Though the editor isn't as advanced as I would like it to be, I hope it can still be useful or educational for other sceners, or even just fun to play with.
How IFS fractals work
Editing IFS fractals is rather difficult, because every little change you make influences the whole result. In order to sculpt a fractal close to what you have in mind, you must understand how IFS fractals really work.
The basic idea is that you start with a point in (2D or 3D) space. You have two or more functions available which transform a point to another location. In a loop, you pick one of those functions, and execute it on the old point. This results in a new point which is part of the fractal, so you draw it. Then you choose a function again, execute it on the new point and you get the next point, etc etc.
Of course, in order to make beautiful fractals, your functions must follow some rules, or you'll end up with thousands of points scattered randomly through space. The most important quality is that the functions should contract, so they should concentrate input points from a wide area into a smaller area. Almost all IFS fractals use affine transformations as functions, although it is possible to use others as well (Google for Apophysis for an opensource program that can do non-affine IFS fractals).
Walking the line: 1 D fractals
If this doesn't make sense, don't worry. We'll go over more concrete examples, starting from the most simple fractal possible: a 1-dimensional IFS fractal with only 1 function :) Imagine a straight line going from minus infinity to infinity, with zero in the middle. That's our 1D "space". We randomly pick a point, say x = 100. Now, we need a function to generate new points from old points: x_new = f(x_old). An affine function in 1D space has the form x_new = A * x_old + B. So our first point is x = 100, our second is A*x + B, the third is A*(A*x+B)+B and so on.
Now, depending on the value of A, several things could happen.
- if A is zero, the new value of x will always be B, so our "fractal" consists of a single point. Not very interesting :(
- if A is 1, then each new point will always be B more than the previous. So we get an endless line of points going to plus or minus infinity. Slightly better but still not much of a fractal.
- if the absolute value of A is larger than 1, the fractal becomes chaotic. For example, if A is -2 and B is 50, we get the following points: 100, -150, 350, -650, 1350, -2650,... It's obvious all future points will be farther and farther away from the origin (x=0), and also farther away from each other. This is because the multiplication with A increases the distance to the origin with each iteration.
- if the absolute value of A is between 0 and 1, the values will converge to one region. For example, if we use A = -0.6 and B = 50, we get this sequence: 100, -10, 56, 16.5, 40.16, 25.90, 34.45, 29.32, 32.40, 30.55, ... This is because A and B now balance each other.
Strange Attractions
If we look at the A*x and the + B parts separately, we can imagine them as two forces: adding B pushes points in one direction, either positive or negative infinity, but with a constant "speed": over the same distance for each iteration.
Multiplying with A (with |A| < 1) pulls points closer to the origin x = 0, but not at a constant speed: if the point is already close to 0, it won't move much. But if the point is very far away from 0, it will be moved much more, proportionally to its distance from 0. So we have A pulling points closer to 0, and B pulling them to plus or minus infinity. If a point is far enough away from 0, then A is stronger than B, but if the point is close enough to 0, then A will be weaker than B. There is one location where forces A and B are exactly the same, this is x = B/(1-A). If your startpoint happened to be that point, all your next points will be the same. But if you choose any other point as startpoint, no matter what, then each new iteration will bring you closer and closer to B/(1-A), without ever reaching it. This point is called the attractor.
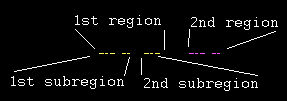
Now, a sequence of points converging to an attractor still isn't a fractal, right? But remember that an IFS fractal should have *two or more* functions! What happens if we have two functions with different As and Bs (each with |A| < 1, of course), and randomly choose between those two when generating the next points? Each function has its own attractor. If we generate thousands of points, there will be times when we select the first function 5, 6 or even more times in a row. This will cause a strong buildup of points around the first attractor. But the same is true for the second function, so we'll have two dense regions on our 1D line.
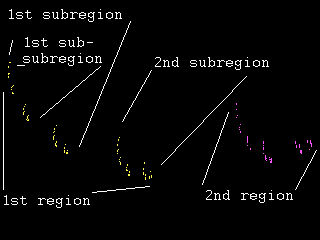
If both B's are different and sufficiently larger than 0, these two regions will be cleanly separated. Imagine two points, one from each region, going through the first function. Now both of them will be in the first region. However, the point that already was in the first region will be closer to the first attractor than the one from the second region. So the first region will also be split in two subregions: one subregion for points whose last two iterations where through the first function, and the other sub-region for points whose next to last iteration was through the second and whose last iteration was through the first function.

So the first region is split in two sub-regions, and in the same way the second will be split. The subregions will also resemble the main regions: if there is one small and one large region (because the A of one function is smaller than that of the other function, and thus converges faster), there will also be one small and one large sub-region in each region. And the sub-regions will also be split in two sub-subregions, who resemble the main regions, and so on and so on. The whole set of the regions and sub-regions is called the strange attractor, this is where all points converge to, no matter where you start.
It is possible, if the B's of both functions do not differ enough, or if the A's aren't small enough, that the two main regions overlap each other. In that case the sub- and sub-sub regions will also overlap and the fractal will look rather fuzzy. It's still a fractal, but it's typically not what you want.
Breaking the first dimension: 2D
1D IFS fractals are rather boring, but once you understand them you're well on your way to understand 2D IFS fractals. 2D fractals use 2D functions, so (x_new,y_new) = f(x_old,y_old). If we limit ourselves to affine functions once again, the functions have this form:
(x_new) = [ a b ] * (x_old) + [e]
(y_new) [ c d ] (y_old) [f]
So the shape is similar to the 1D function, but we use matrices and vectors now: A is replaced by a 2*2 matrix and B by a vector with size 2. The role of B doesn't change much: it is still a force that pulls point to one direction at a constant speed. But A is the key to interesting 2D fractals.
An affine transformation matrix can be used for 3 things: scaling, rotation and skewing.
- Scaling is the same as for 1D fractals: the absolute value of the scale factor should be between 0 and 1, or your fractal will look like random points. There needs to be a force pulling points closer together, to balance the force of the vector.
- The rotation plays a major role in making fractals "interesting". Without rotation, the attractor for a single function would still be a single point somewhere on the plane, but if a function has a small rotation, the attractor for that function will resemble an ellipse. If at least one function has a rotation, the resulting fractal will be more curvy, or look like a spiral.
- Skewing is the transformation that makes a parallellogram from a rectangle. It changes the angle between your X and Y axis. For IFS fractals, a function with skew squeezes one region of the fractal, making it longer and thinner.
Each type of transformation has its own matrix, if you've ever worked with 3D rendering you'll probably know scaling and rotation matrices already. But if you multiply them you get a matrix with the combined functionality, so a single function will usually scale, rotate and sometime skew at the same time.
Smaller, Bigger, Denser, Sparser
Note that everything we learned from the 1D IFS fractals still holds: using 2 functions, you'll have two parts. They may differ in shape, but they'll both have two sub-regions which will differ in shape in the same way, and so on. It's not always easy to see this though. Especially if one function scales fast (much smaller than 1) and the other slow (close to 1), one part will be very small and the other very large. But the large part will also have a small sub-part, which will look almost the same as the small main part. Instead of 2 regions, it will look as if you've a whole sequence of ever-shrinking regions.
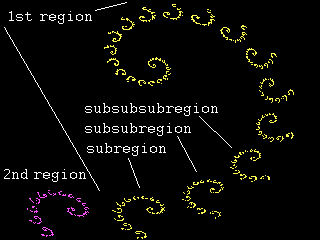
The easiest way to see the regions is by painting them in different colors. When calculating the next point, we choose a function at random. If this is the first function, we'll draw it in yellow, if it's the second we draw in in purple, and so on with other colors if there are more than 2 functions.
If the two regions differ a lot in size, it becomes inefficient to chose randomly between the two functions. If both functions are used the same number of times, the smaller region will have the same number of points as the larger, and will look much denser as a result. The large region will look very sparse, and it will be hard to see the recursive subregions. To fix this, we should not choose the functions the same amount, but weighted towards the size of the resulting regions: more often for a large region and less often for a small one. One way to do this is by putting the 4 corner points of a square with size 1 through the first function, and calculate the surface area of the resulting parallelogram. Do the same with the second function, and if the area of the first is 1/4th of the second, we should pick the first function 1/5th of the times, and the second function 4/5th of the times.
3D: more of the same
Once you understand 2D IFS fractals you know the 3D stuff as well, because everything stays the same, only with an added Z-axis. The B-part becomes a 3D vector pulling points to one direction in 3D space, and the A-part becomes a 3*3 matrix used for scaling, rotation and skewing in 3 dimensions. So conceptually, there's nothing new. When showing the fractal on screen, it's usually best to move or rotate it before the camera or otherwise it might be hard to see it's in 3D (since points lack shading etc).
Here's the core of the drawing routine of the example program Show_IFS that should be in the bonus pack:
for (i = 0; i < 10000; i++)
{
// choose a function randomly, but weighted by the relative size
ran = rand();
r = 0;
while (ran > inIFS.m_limits[r]) r++;
// get the new point
inIFS.m_ifs[r].TransformPoint(point);
// draw the point in the corresponding color
uint32 color = inIFS.m_ifs[r].GetColor();
glBegin(GL_POINTS);
glColor3ub( (color >> 16) & 0xFF, (color >> 8) & 0xFF, color & 0xFF );
glVertex3f(point[0], point[1], point[2]);
glEnd();
}
Not very complex, right? (Of course it's simplified for education's sake, there are many things you can do to make it run faster that will make it more complex as well).
The editor: Do what I want, not what I say
The step from 2D to 3D is very small for generating IFS fractals, but very large for designing them. Most 2D editors I've seen use one of two methods:
- either you have to directly enter the numbers in the matrices/vectors. This is completely unintuitive and unpredictable.
- or, for each function, three points forming a triangle are pulled through each function and displayed. You can change the matrices and vectors by moving the points of those triangles around, but this is cumbersome and still unintuitive, for the following reasons:
- to move/rotate a triangle you've to change all three points, this is slow.
- you can't see the rotations/scale/skew factors making up the matrix, so you can't think about how you need to change them to get the result you want.
- you can't see if skew is used: a skewed triangle is still a triangle, while a skewed square is a parallellogram.
So, to make designing 3D IFS fractals as intuitive and fast as possible, I made the following decisions:
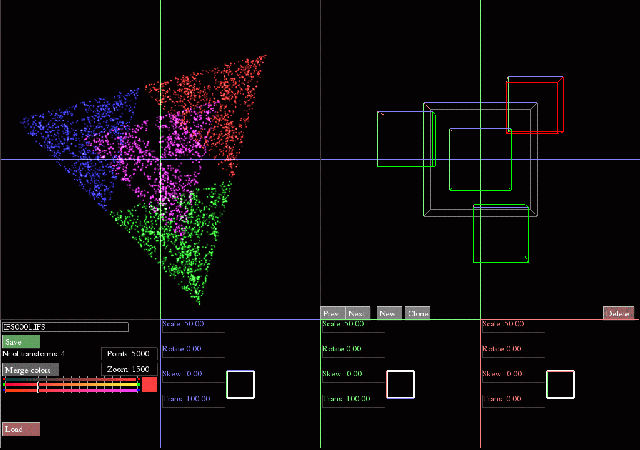
- Show the functions as green cubes, with separate colors for the X/Y/Z axis in one corner, so you can see if they are upside down or tilted etc.
- Show the cubes and the resulting fractal side-by-side, so you can see the relationship between for example a large cube and the resulting large region.
- Moving the camera is done by dragging the mouse over the fractal or the cubes, the two cameras are linked.
- The selected transformation cube is shown in red, and shown again in three small windows from the X/Y/Z direction. The windows are color-coded to the axis.
- The scale, rotation, skew and position of the cube on each axis is shown in the three small windows. You can edit these values by simply dragging with the mouse, and the fractal is recalculated instantly.
- Besides adding a new cube/function, you can also clone an existing one and move that one to a new location. This makes it much easier to build certain symmetric fractals.
One thing I struggled with a lot was the order and choice of the transformations to build the matrix. Should I rotate around the main X/Y/Z axis or around the cubes own X/Y/Z axis? Should I skew first, or rotate first, or move the cube first? In the end, this sequence turned out to give the most predictable results:
- First scale the cube along its own X/Y/Z axis.
- Then rotate it along its own axis. Note that rotation around f.e. the X-axis changes the rotation values for the Y and Z axis, not for the X axis. That's because the values displayed show the angle between the main "world" X/Y/Z axis and the cubes X/Y/Z axis. It's a bit strange, but I usually just look at the cube, not at the values.
- Then skew the cube around its own X/Y/Z axis. Again, skewing around the X-axis changes the angle between the Y- and Z-axis. I usually do this last, just to tweak a fractal a little.
- Then move the cube along the world's X/Y/Z axis. You don't want to work with the cube's local axis after they've been skewed.
Some hints if you want to play with the editor:
- Start with only 2 transformations. It's much easier to get a feeling for the fractals if you start simple. Explore some edge conditions: what happens if you make one cube very large and the other very small? What happens if one is close to the middle and the other far away? What if they're close to each other? Don't forget to rotate them often, since this causes far more changes than moving them around.
- One sure-fire strategy to make a fractal in the shape you want, is to use many small cubes and put them in that shape. This doesn't look very good, but it's a starting point. Try to combine two boxes close together with a larger rectangular one. Look for features in the shape you want which can be approximated with a squeezed/twisted version of the whole. If all else fails, you can glue two fractals together, that's how I made the planets in Heliosphere, since I couldn't make a globe but I could make one half of it.
In the bonus pack you'll find two programs: IFS_Edit, the editor but without source, which allows you to make, save and load fractals, and IFS_Show, a simple (ugly) SDL program with source that loads and shows a saved fractal. You're free to adapt it to use in your own demo, but please optimize/customize it a bit and don't forget to greet me ;)
To show fractals you've saved in the editor, pass the name of the saved file as the first argument to IFS_Show. Some examples are included, try "IFS_Show TwinSpiral.IFS" or "IFS_Show Hugi.IFS".
Seven/Fulcrum