
Marching Cubes Based Polygonisation
Disclaimer
I don't claim this is in any way comprehensive on the subject it aims to cover. There are no guarantees given with this document, except that nothing is ripped. The methods used in this document are by no means the best, nor is the sample source code provided.

Introduction
Hey all! This article is about the marching cubes algorithm, the algorithm used to produce cool effects like metaballs (not to be mistaken for meatballs, which you can find in your local supermarket).
There are some very good articles on the net about marching cubes. You should check out Paul Bourke's page, it is where I learned marching cubes from. Exaflop also has a very good article about it. Bloomenthal's paper "Polygonization of implicit surfaces" is also very clear, and gives a very nice overview of the technique. It perhaps isn't suitable if you're new to the algorithm.
We'll develop an implementation of marching cubes using object orientation, and then apply it to rendering the well known effect of metaballs.
Motivation
Ok, this is my own motivation for marching cubes... I have more or less just come up with it on the spot.
Suppose we have a surface defined by a mathematical equation: E.g. a sphere, r^2 = x^2 + y^2 + z^2, for a sphere of radius r, a point is on the sphere if it satisfies the equation. This is the idea behind marching cubes, we have an equation defining a surface, and we solve it in real time to get a plot of the surface in 3D.
In 2D, if we wanted to plot a circle defined by the equation x^2 + y^2 = r^2, we could use the following approach: for every possible value of x and y see do they satisfy the equation, for those that do, plot the pixel on the screen. This is a bad approach for drawing a circle in 2D, since we can solve the equation explicitly rather than implicitly (i.e. trying every point by trial and error).
However, suppose someone gave us ANY function representing a 2D plot. How would we plot that? The implicit method presents itself, since we don't know how to just generate points on the surface (as we would for e.g. A circle). Once we agree to use the implicit method, the problem is to figure out how to actually draw the solution to the equation on the screen, we need some algorithm to generate polygons so we can draw it. Marching cubes is this algorithm.
Marching Cubes: Polygonisation
First we define a space size, this space is where the points in consideration for inclusion in our surface must reside. We could use a space of x-y-z size 320x320x320 for example.
Next we subdivide the space into a designated number of cubes in each direction, it doesn't have to be the same number in each direction, but it's advisable to keep the length of side of the cubes constant, otherwise you can get skewing of the surface.
A typical number of cubes might be 32x32x32, for our space above this gives us cubes of dimensions 10x10x10. Note that even small looking numbers of cubes like 32x32x32 are very large, 32x32x32 = 2^15 = 32,768 cubes.
The number of cubes and space size define how exact our constructed surface will be. The length of side of a cube is what counts in how accurate the constructed surface is, above 10x10x10 would probably give a pretty crappy looking surface. However, if we made our space a bit smaller, e.g. 160x160x160 it'd probably be very accurate.
Now, for marching cubes to work, we must be able to answer one question given any point and a surface: Is this point inside the surface? We'll discuss answering this question in a moment, suppose for now, we always can.
We now generate a the mesh of triangles to represent our surface.
Here is how it is done: for every vertex of every cube, we check is that vertex inside or outside the surface. This results in the fundamental cube configurations:
| (i) | The cube is totally inside the surface. |
| (ii) | The cube is totally outside the surface. |
| (iii) | Some of the cube's vertices are inside, and some are outside of the surface (i.e. it intersects it). |
The first two cases give us no information about rendering the surface. The third, however, if some are inside and some are outside, lets us find the intersection of the surface and the sides of the cube and generate some triangles to represent the surface at that intersection. To understand this here's a diagram:
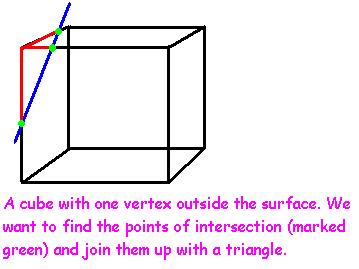
(btw, the surface is just represented by a line in this image, of course, it should be drawn in 3D)
So, if we can find the intersection of the surface and the cube sides, we're all set to generate the mesh. There are two ways to do this, we'll see the second one when we implement metaballs, the first one is binary search. Binary search works since we can always ask is the point inside or outside, and so we refine the estimate of the intersection of the surface and cube in the normal way.
So now we can generate those triangles to represent the surface as follows: Since every vertex of a cube can be either inside or outside the surface there are 256 possible triangulations, two of these are trivial, all outside, and all inside. So we have 254, as it turns out, by reflections and rotations of the cube there are only 15 different triangulations we have to special case in our code (e.g. we'd only have one special case for any one vertex of the cube outside the surface only, cutting our work down by 8 cases).
It sounds pretty boring to code the 15 special cases, the kind of boring code I try to avoid, so instead I do it a simpler way.
On Paul Bourke's home page he uses some look up tables to get the triangulation. Here is how we do it: Each vertex outside is represented by a 1 and each vertex inside is represented by a 0, in binary, and we must have a consistent labeling system for our vertices. Then we generate an 8-bit index into the edge intersection table.
An example: Suppose vertices 5, 0 and 6 were outside (we number the vertices of a cube 0, 1, ..., 7). Then we'd generate this index: 01010001. We then index an edge intersection table with that, and it gives us a 12 bit number (since a cube has twelve sides) telling us which sides of the cube are intersected, e.g. if edges 0, 1 and 2 were intersected then this number would pop out of the table: 000000000111. A '1' representing an intersected edge for each bit of the number. Now we have to actually find the intersection and we have the mesh.
Finally we use our index again this time to index a triangulation table, which tells us which vertices to join to which in the mesh. These tables are provided with the sample source, and we'll see below exactly how to do the above.
We've been doing things on a cube by cube basis, does this mean to actually generate the surface we have to go through EVERY cube in the space and check if its vertices are inside or outside the surface? Wouldn't that be very slow? We don't go through every cube in the space, because doing so would be too slow for realtime apps. Instead we use depth first search.
We simply note that every cube which intersects the surface is incident to at least one other cube which intersects the surface. So, given one intersecting cube we can just test all of the cubes touching it, and all the ones touching them, etc. So it'll be recursive. Notice that each cube has eighteen incident cubes BUT we don't need to recursively check all of them, only the ones stuck to its 6 faces, since when they recurse they will test the ones that it would have tested if we called it with all eighteen incident cubes. The termination condition for this recursive algorithm is when we reach a cube we have already encountered. Essentially what we are doing here is drawing the connected components of a graph.
The only very slight draw back of the above is that we have to be able to supply the polygonisation routine with an intersecting cube, we'll see ways to do this later on.
Btw, there is another way of avoiding testing every cube in the octree using bounding boxes, but I've never coded this and don't know the details of how it works.
Metaballs: Defining The Surface
If you don't know how and why blobs work, you could try reading my article on them in Hugi Diskmag #21 (available at www.hugi.de).
First of all suppose we already have our marching cubes based mesh generator thingy, and that we just need to give it a function to tell it whether a point is inside or outside the surface and a function which finds the intersection of a cube and the surface for it. We pass the mesh generator these functions and it works away fine on the surface which these functions have defined. All we are left with is writing these functions to pass to it.
class Point3D
{
public:
int x, y, z;
Point3D(int x = 0, int y = 0, int z = 0)
{ this->x = x; this->y = y; this->z = z; return; }
};
The above class is used for declaring 3D points.
We want to do metaballs, so we'll develop a class to represent our metaball surface, in the code I call this class SphereSurface, here it is:
class SphereSurface
{
int nSpheres, nCells;
float minPotential;
Point3D *coords, stepSize, spaceSize;
public:
float *potentialBuf;
SphereSurface(int nSpheres, int radius, int nCells,
Point3D spaceSize, Point3D *coords);
float getPotential(Point3D p);
bool outside(Point3D p);
Point3D getIntersection(Point3D p1, Point3D p2);
~SphereSurface();
};
This is treated as a black-box by our marching cubes code which just uses two methods: getIntersection and outside. However, we need to develop code for this, it's simple, to do this.
Let's start with the constructor:
SphereSurface::SphereSurface(int nSpheres, int radius, int nCells,
Point3D spaceSize, Point3D *coords)
{
this->nSpheres = nSpheres;
this->nCells = nCells;
this->stepSize = stepSize;
this->coords = coords;
this->spaceSize = Point3D(spaceSize.x / 2, spaceSize.y / 2,
spaceSize.z / 2);
this->stepSize = Point3D(spaceSize.x / nCells, spaceSize.y / nCells,
spaceSize.z / nCells);
minPotential = 1 / (float) (1 + (radius * radius));
potentialBuf = new float[nCells * nCells * nCells];
memset(potentialBuf, 0, nCells * nCells * nCells * sizeof(float));
return;
}
We need to define the surface, so naturally we tell it the number of metaballs and their radii. Now, some data which must be the same between the surface and the marching cubes code, the number of cubes in every direction (nCells), and spaceSize, which is the x-y-z size of our surface space. Finally a pointer to the coordinates of the metaballs is passed. minPotential is the potential every point on the surface has, the reason there is a (1 + ...) will become apparent in a moment.
Our potential function is called getPotential:
float SphereSurface::getPotential(Point3D p)
{
if(p.x < -spaceSize.x || p.y < -spaceSize.y || p.z < -spaceSize.z || p.x
>= spaceSize.x || p.y >= spaceSize.y || p.z >= spaceSize.z) return -1;
int ind = ((p.z + spaceSize.z) / stepSize.z) * nCells * nCells +
((p.y + spaceSize.y) / stepSize.y) * nCells +
((p.x + spaceSize.x) / stepSize.x);
if(potentialBuf[ind]) return potentialBuf[ind];
float total = 0;
for(int i = 0; i < nSpheres; i++)
total += 1 / (float) (1 + (
((p.x - coords[i].x) * (p.x - coords[i].x)) +
((p.y - coords[i].y) * (p.y - coords[i].y)) +
((p.z - coords[i].z) * (p.z - coords[i].z))));
potentialBuf[ind] = total;
return total;
}
You can ignore the references to potentialBuf if you like, it's just for a tiny bit of extra speed.
The (1 + ...) is here to prevent divide by zeros, so above we must compensate.
Now our outside method:
bool SphereSurface::outside(Point3D p)
{
if(getPotential(p) < minPotential) return 1;
return 0;
}
Finally comes the getIntersection method. Remember I described a binary search method for find the intersection between any surface and a cube, that method is very general, but also very slow. Instead we use our knowledge of metaballs to give us a fast algorithm to find an approximate intersection.
Here is how it works:
If we know the potential at two points p1 and p2, and we know it varies linearly between p1 and p2, that is, the potential increases in uniform increments between p1 and p2 then we can use linear interpolation to find the exact intersection of the surface and cube side. Note that our potential function, 1/r^2 does NOT vary linearly in space, however, if the two points which we are interpolating between are sufficiently close together, then it won't be a bad approximation, actually, if the points we were interpolating between were ever far enough apart to make the approximation seriously bad, it'd probably mean are cubes were so big the polygonisation would be horrible anyway. Having said that, this approximation's accuracy depends on how much your potential function varies between two points in space, for some functions it might look really crappy even with lots of cubes. Anyway, take a look at the graph of y = 1/x^2 as x gets large it nearly varies linearly.
*------|-------*
p1 S p2
The surface's potential is at a coordinate we want to find and is marked S, call the coordinate of the intersection Sp and the potential at this coordinate Sv.
Call the potential at p1 v1 and v2 at p2. We hope the potential varies linearly between p1 and p2, so, for each unit change in coordinate, the potential varies by a certain amount, call it P:
p2 - p1
P = -------
v2 - v1
We know the potential at S (minPotential), we want to find the number of units away from p1 we are, which is: P * (Sv - v1). Finally we want to find the actual point so it is p1 + P * Sv. Expanding this we have:
(p2 - p1) * (Sv - v1)
Sp = p1 + ---------------------
v2 - v1
and in implementation:
Point3D SphereSurface::getIntersection(Point3D p1, Point3D p2)
{
Point3D t;
float v1 = getPotential(p1), v2 = getPotential(p2), mp = minPotential;
t.x = p1.x + (mp - v1) * (p2.x - p1.x) / (float) (v2 - v1);
t.y = p1.y + (mp - v1) * (p2.y - p1.y) / (float) (v2 - v1);
t.z = p1.z + (mp - v1) * (p2.z - p1.z) / (float) (v2 - v1);
return t;
}
Now we have our surface fully defined for our marching cubes code, all we have to do is code that. First though we'll see how all this fits together:
int nCells = 20, nBlobs = 6, blobRadius = 18;
Point3D spaceSize(160, 160, 160), *coords = new Point3D[nBlobs];
Point3D *mesh = new Point3D[5 * nCells * nCells * nCells];
SphereSurface surf(nBlobs, blobRadius, nCells, spaceSize, coords);
CalcMesh
I allocate 5 * nCells * nCells * nCells for mesh, because each cube can contribute a maximum of 5 triangles to the mesh, although I don't think this could ever happen in practice. You could probably get away with 3 * nCells * nCells * nCells, but it is maybe a little dangerous.
The CalcMesh class is what we want to code next. You see, it can take any surface at all, once it provides certain methods. In this case it takes the SphereSurface object surf (note that CalcMesh is a template class).
Marching Cubes: Implementation
Now we have to actually implement our CalcMesh class, actually this is very easy.
Here's the class:
template
Ok, the first bit of data is just the size of the space and the x-y-z size of each cube (spaceSize and stepSize, respectively).
Now comes a pointer to the surface, surfType being defined when the class is instantiated, we need a pointer to the class so we can call two of its methods: surface->outside(blabla), and surface->getIntersection(blabla).
Now we have the getIndex function, which generates an index into the edge intersection table, remember, it does this by checking which vertices of the cube are inside or outside the surface, the code is simple:
template
For every point it sets the particular bit corresponding to that vertex.
The triangulate method generates the triangulation of the surface at one cube. The triangulation comes directly from the table. Strictly speaking, a triangulation of a convex polygon, P = { v1,v2,..,vn,v1 } is a subdivision of the polygon into triangles with non-intersecting sides, but we don't always get polygons when we find the surface/cube intersection, sometimes just two separate triangles, but we still need the tables to tell us which vertices make up each triangle. It's worth doing some examples on paper to get a full understanding of this, imo. Anyway, here's the code:
template
It's pretty big, each line just checks if a particular bit is set in the edge intersection table (edgeTab), and if it is it finds the intersection of the surface and the cube. The arguments to getIntersection are "hard coded", they depend on how we label the cube's edges and vertices. All they are doing is looking at the edgeTab, seeing if this edge is intersected, and then using getIntersection on the two vertices which this edge joins. Then I add the vertices to my mesh. They are added in the order that they are for backface removal using OpenGL. triTab just tells the mesh which vertices to join to which, each triangle for rendering is then given by each set of three consecutive elements in mesh.
Now, the last thing we have to code is the function to recursively call triangulate for each cube intersecting the surface, here it is:
template
What this does is as follows, we give it a cube's top-left-back coordinate, it then generates the cube's vertices, which are stored in the variable s. Then it generates an index for the cube, and a triangulation, and then recurses.
The buffer visited is a "3D" buffer used to test which cubes we've visited.
Now, the only thing that we have left is to give this function an intersecting cube. To do this I wrote a little function:
template
Again, we give it the top-left-back corner of a cube, it moves left until it finds an intersecting cube, and then returns the x-coordinate of a cube of the same x and y as the cube it was given which intersects the surface. It's a good idea to call this function with coordinates which are pretty much always going to be close to an intersecting cube for speed purposes.
General Comments
Something to note about the algorithm is that we can construct a surface at any resolution, i.e. it can be as accurate or inaccurate as we please.
Finally, in most demos metaballs are the only type of surface rendered using marching cubes. It's not too hard to do lots of other things. You just have to supply CalcMesh with the intersection and outside methods. An example, we could render a surface which whose potential function was defined with respect to the distance a point was from a 3D sine curve.
MetaCylinders
I hadn't planned to put this in, but I thought I might as well show that we can render general surfaces.
You can use the code provided to render cool looking meta-cylinders which melt together at junctions by defining a potential function which decreases with distance from an axis. So we can do some math to figure this out, I'll do an arbitrary axis first, then a simpler axis.
U
/│\ D
├─┬─────────*(x, y, z)
├─┘ /
│ /
Q │ /
│ / V
│Ó /
│/
O
O is the origin of the cylinder.
U is any vector representing the axis of the cylinder.
V is the vector from O to (x, y, z).
(x, y, z) is the point whose potential we want to find, by finding its
distance, D, from the axis.
So to do this we can use pythagoras.
|V|^2 = D^2 + Q^2
But we don't know Q. To find Q we can use some basic trig and linear algebra:
Q
cosÓ = -
|V|
Using the dot product of U and V:
|U| * |V| * cosÓ = U.x * x + U.y * y + U.z * z
Q
=> |U| * |V| * - = U.x * x + U.y * y + U.z * z
|V|
=> |U| * Q = U.x * x + U.y * y + U.z * z
U.x * x + U.y * y + U.z * z
=> Q = ───────────────────────────
|U|
If we keep U a unit vector we can calculate Q with a single dot product.
By pythag:
|V|^2 = |D|^2 + |Q|^2
=> |D|^2 = |V|^2 - |Q|^2
Now for, say, a vertical axis U = (0, 1, 0), the equation for Q becomes:
Q = y
You can easily get two fused cylinders (like at the heading of this doc) using this method. Although they'll be infinitely long, to stop this just check the distance a point is along the axis from the origin of the cylinder.
Sample source code
The sample source code provided is written in C++, it uses OpenGL for rendering. The code in the file mballs.cpp is a little infested with literals, most of them are quite obvious, although they really shouldn't be there. There has been no effort put into optimising either the code in mcubes.cpp or mballs.cpp, besides, it'd be much harder to understand the code if it was cleverly optimised.
The implementation is quite slow.
There aren't any bugs that I know of in the marching cubes code. I'm not sure about the whole tutorial, but that part should be fine. And any bugs, anywhere, should be very minor (famous last words :)).
If you play with the code a little, things might start going wrong, there are a few common things which can happen, which aren't bugs in my code:
| (i) | Strange clipping of the surface can happen if the space is too small, what happens is, all of the surface inside the space is rendered, but the cubes which are outside the space (and would finish off the surface) are excluded. |
| (ii) | Sometimes you might find parts of the surface flicker (not flickering polygons mind), this is because the recursive function to generate the mesh hasn't been called with the right arguments, it has to be given a cube which intersects the surface. In metaballs, this usually happen to a single metaball, i.e. the whole metaball flickers. |
| (iii) | Stack overflow. This happens if the surface is really big, causing the recursion to get too deep. |
Misused Terms
I misused/made up some terms for this doc, just to let you know:
Potential function: Usually called a "field function"
Potential: Usually called a "field value"
Surface Space: Usually called a "scalar field" or "density field". I think it is called a scalar field because each point in it has an associated scalar (computed using the field function).
The latter term I believe is because, Blinn, the guy who originally did this type of modeling got the surface by the adding up of Gaussians based on the electron's density field and then raytraced his result. Hence the term "density field".
Conclusion
Well... I hope you learned from this article, don't hesitate to drop me a line, I like email. My time is somewhat limited by high school though, so I might take a while to reply. I'd be really grateful if you could point out any mistakes in this doc to me too.
Last thing, if you want to use this code in a demo (which I do not recommend because it's so slow) don't feel you have to credit me, after all, once you have read the tut and understand it, it's basically your code. You should probably say that you used the tables from Paul Bourke's page though, since they aren't mine to give away (see info at top of source file tables.h).
I have to stop now, it's too late (early?) to be writing docs...
- paradox / vivid
- Nicholas Nash
- nnash@stokes2.thphys.may.ie
- nash@cfxweb.net
- paradox@the-vivid-ones.de