Drawing Triangles. Rasterization Tutorial
Hello all, since I got some requests from newbies for help with coding triangle drawers, I've decided to write an article.
I know that Fatmap and FatmapII exist. I've also heard that the articles by Chris Heker are good. I've never read them, though.
Fatmap and FatmapII explain how to optimize the rasterizer. They hardly show how to implement things, and there is almost no explanation at all. I personally think that it scares many newbies. I've never seen a good triangle-filling tutorial, most of the ones I've seen use the scan conversion method and store the result to buffers, then just interpolate the values in the buffers. That's really not effective. It's way better to interpolate all values at one run.
I'll try to explain everything that may need to be coded, from a flat-filler to a perspective correct texturemapper, zbuffer, wbuffer, subpixeling, subtexeling, scanline subdivision, and all that comes with it.
Oh, and I'll be using only floating point.
Some theory and practice
First I must tell you all about the magical word interpolation. What does interpolation mean? Why do I have to use it? Who invented it? And why do I read this article?
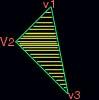
Interpolation means getting from point A to point B in N steps. I'll answer the rest of the questions later in the article. It is not the only way to fill a triangle. In my article I will interpolate the x values over the triangle edges and then draw a horizontal line between the two values Xleft and Xright. That horizontal line between the two values is called a scanline. Here's an example of it, the yellow lines are the scanlines filling the triangle.

You are probably thinking while looking at that lousy picture, it looks easy as hell. You're right! The only knowledge you should have is some linear algebra and how to plot a pixel on the screen. In my drawing of the first triangle the V2 is on the left side, which means that V1 to V3 edge is the right side. It is important to know on what side an edge is for coding a 100% working triangle.
Note! We'll add the subpixeling later at the final stage of our flat triangle.
Ok, now let me describe the steps for making a triangle filler:
1. We need to define some structure for the vertex:
struct Vertex {
float x, y;
};
float Left_dXdY, Right_dXdY,
LeftX, RightX;
byte *dest_ptr;
You'll get some explanation for those variables.
2. We'll give the triangle the following data:
void FlatTriangle(Vertex *V1, Vertex *V2, Vertex *V3, byte *dest);
I just love pointers.
3. Sort the vertices (V1,V2,V3) by their Y values.
V1->y = top
V2->y = middle
V3->y = bottom
Pseudo:
if (V1->y > V2->y) swap(V1,V2);
if (V1->y > V3->y) swap(V1,V3);
if (V2->y > V3->y) swap(V2,V3);
4. Now let's define three more variables y1i, y2i and y3i, they stand for:
y1i - y1 integer value
y2i - y2 integer value
y3i - y3 integer value
I'll use the ceil function, to fit our subpixeling later.
long y1i = ceil(V1->y);
long y2i = ceil(V2->y);
long y3i = ceil(V3->y);
dest_ptr is a pointer to our virtual screen (buffer), we calculate it as followed:
dest_ptr = &dest[y1i*320];
That way we will avoid multiplying each Y by 320 to get the current offset in our virtual screen. You'll see more details in section nine.
For the ones of you who don't know what ceil is, ceil just rounds the value upwards, like:
ceil(1.2) = 2
ceil(-0.3) = 0
ceil(1) = 1
5. It's time to check if we have more than a zero height triangle.
if (y1i==y3i) return;
6. Now we have to make 3 slopes calculations,
dXdY - means deltaX/deltaY
dXdY_V1V2 - means dXdY for the edge V1 to V2.
float dXdY_V1V3 = (V3->x - V1->x) / (V3->y - V1->y);
float dXdY_V2V3 = (V3->x - V2->x) / (V3->y - V2->y);
float dXdY_V1V2 = (V2->x - V1->x) / (V2->y - V1->y);
7. We got to the stage where we have to decide whether V2 is on the left side or the right one. We could do that by finding the V4, and check the distance from V4 to V2, distance = V4.x - V2.x. That distance is marked with the white color.
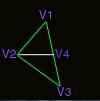
Sounds easy, huh?
We'll use the linear interpolation formula I(t) = A + t(B-A). t is the interpolation factor. -1<=t<=1. When t=0 the result is A, when t=1 the result is B, etc...
We know that that V2.y = V4.y and V4 is on the edge (V1V3) from V1 to V3.
If we find the t at V2.y, we have the V4.
y = V1->y + t(V3->y - V1->y)
y=V2->y
V2->y - V1->y = t(V3->y - V1->y)
(V2->y - V1->y)
t = ---------------
(V3->y - V1->y)
V4->x = V1->x + t(V3->x - V1->x)
V4->y = V2->y
float distance = V4->x - V2->x;
if (distance>0) then the middle vertex is on the left side (V1V3 is the longest edge on the right side), and if (distance<0) then V1V3 is on the left side.
8. Also we need a routine which draws a segment. A triangle is made out of two segments.
The first segment is from y1i to y2i and its color is red, the second one is from y2i to y3i and its color is blue.
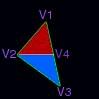
9. Before we make our DrawSegment routine we have to define some external variables: Left_dXdY, Right_dXdY, LeftX, RightX of the type float of course and dest_ptr of the type byte. Just to remind you again, I'm using ceil for subpixel accuracy, which will be explained later in this chapter.
void DrawSegment(long y1, long y2, byte color) {
for (long y=y1; y<y2; y++) {
long x1 = ceil(LeftX);
long x2 = ceil(RightX);
byte *dest=dest_ptr+x1;
for (long x=x1; x<x2; x++) *dest++=color;
dest_ptr+=320; // avoiding the multiply by 320
// Interpolation of X coordinates over left and right edges.
LeftX+=Left_dXdY;
RightX+=Right_dXdY;
}
}
Note!!!
If you plan to do an asm version of the inner loop, "for (long x=x1; x<x2; x++) *dest++=color;", make sure to check if the length=x2-x1 is bigger than zero. I've had some problems with it once, don't make the mistakes I made.
10. A special case is y1i=y2i, I'll give you an example only when the V2 is on the left side.
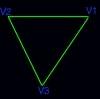
Pseudo:
Right_dXdY = dXdY_V1V3;
The long right edge won't change in the whole triangle so there's no use setting it every time.
if (y1i==y2i) {
Left_dXdY = dXdY_V2V3;
LeftX = V2->x;
RightX = V1->x;
DrawSegment(y1i, y3i, color);
return;
}
Ah well, let's finish that code for the whole triangle.
if (y1i<y2i) {
Left_dXdY = dXdY_V1V2;
LeftX = V1->x;
RightX = V1->x;
DrawSegment(y1i, y2i, color);
}
if (y2i<y3i) {
Left_dXdY = dXdY_V2V3;
LeftX = V2->x;
DrawSegment(y1i, y2i, color);
}
This was the case for when V2 is on the left side. You should code your own special code for when the V2 is on the right side. I'll still add some source code, and include some at the end of this chapter. I suggest coding it from the start. I bet that you'll get the idea. If you get a little confused, that's just fine, remember, paper is your best friend, always draw and think things over again and again until you get it.
TIP!!! As always there is a faster way for checking on which side the V2 is. Before I show it you, I must thank Kalms for showing it me among many more interesting things, thanks. You could compare the slopes, if dXdY_V1V2 is bigger than dXdY_V1V2 then V2 is on the left side of the triangle.
Subpixel accuracy
Here comes one of the coolest things, subpixel accuracy. Think to yourself, how do I know if I should put this pixel or not? I hope it's clear I'm talking about fractional values, like (0.6, 1.3), any ideas? Thought so.
hotlot - that red spot, located at (0.9999, 0.9999) of each pixel.
The rule is simple, only when the pixel touches the hotlot can it be drawn.
This is our pixel grid 6x5:
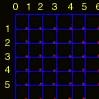
Let's see what pixels should be drawn from our line, which goes approximately from P1(2.4, 0.3) to P2(4.6, 4.8).
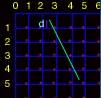
You need to calculate the distance from the current y position (0.3) to the hotlot's y (0.9999). So, let's do it:
For doing things in a more comfortable way we say that the hotlot is at (1,1) of each pixel.
We know that the distance is 0.7,
distance = ceil(P1.y) - P1.y;
distance = ceil(0.3) - 0.3 = 1 - 0.3 = 0.7;
Tada!
dXdY=(P2.x - P1.x)/(P2.y - P1.y);
LeftX = P1.x + distance*dXdY;
Now our X is at the correct position and the Y as well. There's only a tiny problem, the X has a fractal part as well. No fear, you can just ceil(x) as well.
Now that we calculated the intersection with Y=1, from now on every Y skips entire pixel, skips 1 every time, until the last Y that is, you mustn't draw the last Y(P2.y), because, as you can see, it does not have any change to get to ceil(P2.y), so, leave it alone!
So, we draw the pixels: (3,1), (4,2), (4,3) and (5,4).
Try looking at the picture again.

Some code for the lazy ones
Don't be tempted, go and try to do your own code, get it here only if you tried more than three times by yourself. Just think of it as a minor coding challenge.
#define XRES 320
typedef struct
{
float x, y;
} Vertex;
float Left_dXdY, Right_dXdY,
LeftX, RightX;
typedef unsigned char byte;
byte *dest_ptr, *dest;
#define SUB_PIX(a) (ceil(a)-a)
void DrawSegment(long y1, long y2, byte color);
void Swap (void * a, void * b);
void Flat_Triangle
(Vertex *v1, Vertex *v2, Vertex *v3, byte color, byte *where)
{
if (v1->y > v2->y) Swap(&v1, &v2);
if (v1->y > v3->y) Swap(&v1, &v3);
if (v2->y > v3->y) Swap(&v2, &v3);
long y1i=ceil(v1->y);
long y2i=ceil(v2->y);
long y3i=ceil(v3->y);
if (y1i==y3i) return;
float prestep;
dest_ptr = &where[y1i*XRES];
float dXdY_V1V3=(v3->x - v1->x) / (v3->y - v1->y);
float dXdY_V2V3=(v3->x - v2->x) / (v3->y - v2->y);
float dXdY_V1V2=(v2->x - v1->x) / (v2->y - v1->y);
bool mid = dXdY_V1V3<dXdY_V1V2;
// if dXdY_V1V3 slope is bigger than dXdY_V1V2
// then v2 is at the left side of triangle
if (!mid) {
// v2 is at the left side
prestep = SUB_PIX(v1->y);
Right_dXdY = dXdY_V1V3;
if (y1i==y2i) {
Left_dXdY = dXdY_V2V3;
LeftX = v2->x + SUB_PIX(v2->y)*Left_dXdY;
RightX = v1->x + prestep*Right_dXdY;
DrawSegment(y1i, y3i, color);
return;
}
if (y1i<y2i) {
Left_dXdY = dXdY_V1V2;
LeftX = v1->x + prestep*Left_dXdY;
RightX = v1->x + prestep*Right_dXdY;
DrawSegment(y1i, y2i, color);
}
if (y2i<y3i) {
Left_dXdY = dXdY_V2V3;
LeftX = v2->x + SUB_PIX(v2->y)*Left_dXdY;
DrawSegment(y2i, y3i, color);
}
}
else
if (mid) {
// v2 is at the right side
prestep = SUB_PIX(v1->y);
Left_dXdY = dXdY_V1V3;
if (y1i==y2i) {
Right_dXdY = dXdY_V2V3;
LeftX = v1->x + prestep*Left_dXdY;
RightX = v2->x + SUB_PIX(v2->y)*Right_dXdY;
DrawSegment(y1i, y3i, color);
return;
}
if (y1i<y2i) {
Right_dXdY = dXdY_V1V2;
LeftX = v1->x + prestep*Left_dXdY;
RightX = v1->x + prestep*Right_dXdY;
DrawSegment(y1i, y2i, color);
}
if (y2i<y3i)
{
Right_dXdY = dXdY_V2V3;
RightX = v2->x + SUB_PIX(v2->y)*Right_dXdY;
DrawSegment(y2i, y3i, color);
}
}
}
inline void DrawSegment(long y1, long y2, byte color)
{
long x1, x2, y;
for (y=y1;y<y2;y++) {
x1 = ceil(LeftX);
x2 = ceil(RightX);
dest = dest_ptr+x1;
while (x1++<x2) *dest++=color;
LeftX+=Left_dXdY;
RightX+=Right_dXdY;
dest_ptr+=XRES;
}
}
#pragma aux Swap = \
"mov ebx, [eax]"\
"mov ecx, [edx]"\
"mov [edx], ebx"\
"mov [eax], ecx"\
parm [eax] [edx] \
modify [ebx ecx];
Get your object shaded
Ok, I'll show you in brief how to do flat-shading. The ideal is having your face normals in object space.
Directional Light
Directional light means having just a light vector which lights only in one direction. It could be done just by finding the cosine of the angle between the light vector and the face's normal.
Pseudo:
normalize(light_vector);
(your face normals are already normalized)
You need to normalize your light_vector only if you want to change its direction, if you don't then just normalize it in your start up code.
float dot=DotProduct(light_vector, face_normal);
if (dot<0) dot=0;
if (dot>1) dot=1;
color = dot*max_intensity;
Omni Light
Omni light is very much done like directional light, only that it lights in all directions.
Pseudo:
Precalculate the middle point of each face, just take the average of all the 3 points making a face:
MiddleX = (P1.x + P2.x + P3.x)/3;
Do the same for Y and Z.
light_vector = omni_point - face_middle;
normalize(light_vector);
float dot=DotProduct(light_vector, face_normal);
if (dot<0) dot=0;
if (dot>1) dot=1;
color = dot*max_intensity;
Theory about gouraud
Hmm, you're still here? Don't you have a...? Great.
Have you ever asked yourself what gouraud means? Gouraud means that you interpolate the vertex's intensities.
Let me give you an example of what gouraud is really about. You want to use 3 colors in a line the length of which is 9, like that:
A - color number 1
B - color number 2
C - color number 3
AAABBBCCC
As you can see the change in color is linear, remember what a slope is?
A slope is a linear change of one function with dependency over another.
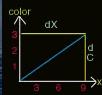
dCdX = delta_Color/delta_X;
Like in this picture, the blue line is the dCdX, which is in our case dCdX=3/9.
color_start = 1;
color=color_start+dCdX*pixel_number;
As you can see,
when pixel_number=1, then color=1;
when pixel_number=3, then color=2:
when pixel_number=6, then color=3.
So we could do:
dCdX = (c2-c1)/(x2-x1);
color = color_start;
for (int x=x1; x<x2; x++) {
putpixel(x, color);
color+=dCdX;
}
We're interpolating the color over as a function of x.
It's like in some physics, you want to get to certain velocity in number of steps, so, the formula is v = v0 + at.
t - time a - acceleration (slope), linear change of velocity in certain time dV/dT v0 - the initial velocity v - the final velocity
dVdT = (v2-v1)/(t2-t1);
v = initial_velocity;
for (int t=t1; t<t2; t++) {
v+=dVdT;
}
Pretty straightforward I guess.
Constant gradients (deltas)
So far we know that we need to interpolate the intensity (color) as well as the X coordinate over triangle edges. I'll show you from the start the faster way doing gouraud, which relies on Teles' rule. It says, two lines that are coming out of a mutual point have the same proportion (ratio).
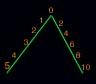
On the left line the slope=1 while in the right line the slope=2, the initial value=0, so, Value = InitValue + Slope*step.
As you can see the ratio of the right line's values divided by the left line's values are equal.
(right) 2 4 6 8 10
--- = --- = --- = --- = --- = 2
(left) 1 2 3 4 5
Any proportion you'll do will be equal for the whole triangle,
/\
a / \A
b/ \B
c/ \C
d/ \D
e/ \E
a=1 b=2 c=3 d=4 e=5
A=2 B=4 C=6 D=8 E=10
A B C D E
--- = --- = --- = --- = ---
a b c d e
You could have also said:
a A
--- = ---
b B
I think you got it by now.
Now let's calculate dCdX, which is constant for the whole triangle:

Let's look at the picture again. We need to calculate both now, the Color and the X coordinate at V4.
I hope you still remember our magical formula:
I(t) = A + t(B-A)
y = y1 + t(y3-y1)
y=y2 (remember?)
(y2-y1)
t = -------
(y3-y1)
(V2->y - V1->y)
t = ---------------
(V3->y - V1->y)
V4->x = V1->x + t(V3->x - V1->x)
dX = V4->x - V2->x
dX = t(V3->x - V1->x) + V1->x - V2->x
Let's plug the "t" into the equation:
(V2->y - V1->y)(V3->x - V1->x)
dX = ------------------------------ + V1->x - V2->x
(V3->y - V1->y)
I'm getting out of screen space now, so I'll use:
x1,y1,c1 for V1
x2,y2,c2 for V2
x3,y3,c3 for V3
x4,y4,c4 for V4
(y2 - y1)(x3 - x1)
dX = --------------------- + x1 - x2
(y3 - y1)
Now let's multiply the equation with (y3 - y1):
Equation 1:
(y3-y1)dX = (y2 - y1)(x3 - x1) + (x1 - x2)(y3-y1)
To calculate dC, we just have to replace X values with C(color):
Equation 2:
(y3-y1)dC = (y2 - y1)(c3 - c1) + (c1 - c2)(y3-y1)
To calculate dC/dX, you have to divide equation 2 by equation 1:
(y3-y1)dC = (y2 - y1)(c3 - c1) + (c1 - c2)(y3-y1)
--------- --------------------------------------
(y3-y1)dX = (y2 - y1)(x3 - x1) + (x1 - x2)(y3-y1)
Ú--------------------------------------------------------¿
³ ³
³ dC (y2 - y1)(c3 - c1) + (c1 - c2)(y3-y1) ³
³dCdX = ---- = -------------------------------------- ³
³ dX (y2 - y1)(x3 - x1) + (x1 - x2)(y3-y1) ³
³ ³
³ ³
À---------------------------------------------------------
In case you were wondering why you should use that long expression, you won't have to make special codes when y1=y2 for example, it will always work.
Gouraud in practice
That's the easiest part, just add a few more external variables:
float Left_dCdY, LeftC, dCdX;
Calculate the dCdX after checking that y1!=y3, and also:
float dCdY_V1V3 = (V3->c - V1->c) / (V3->y - V1->y);
float dCdY_V2V3 = (V3->c - V2->c) / (V3->y - V2->y);
float dCdY_V1V2 = (V2->c - V1->c) / (V2->y - V1->y);
As you can see the division by Y deltas (V3->y - V1->y), (V3->y - V2->y), (V2->y - V1->y) repeats itself, you could use reciprocals:
a 1
--- = --- * a
b b
Do the same for your dXdY and dCdY deltas, it will make things faster. Interpolate only over the left edges as you probably know that for now, in all places you have those:
Left_dXdY = something
LeftX = something
Just add:
Left_dCdY = something with Color parameter instead of X
LeftC = likewise
So if you had:
Left_dXdY = dXdY_V2V3;
LeftX = v2->x + SUB_PIX(v2->y)*Left_dXdY;
You should now have:
Left_dXdY = dXdY_V2V3;
Left_dCdY = dCdY_V2V3;
LeftX = v2->x + SUB_PIX(v2->y)*Left_dXdY;
LeftC = v2->c + SUB_PIX(v2->y)*Left_dCdY;
You need to interpolate the color over the left edge for getting the initial color.
For each scanline you just do:
color = LeftC;
for (int x=x1; x<x2; x++) {
*dest++=(int)color;
color+=dCdX;
}
Type casting is pretty slow, for this kind of operation it would be nice to use Fixed Point math.
How about some lights in it?
The lighting is more or less just like in flat-shading with only one difference: each vertex has its own normal. It's easy as hell to calculate a vertex's normal, you just count in how many triangles this vertex is used, add all the triangle's normals this vertex is in, divide them by how many times this vertex appears, and normalize.
Pseudo:
for (Vertex_Number=0; Vertex_Number<Number_Of_Vertices; Vertex_Number++) {
int count = 0;
vector triangle_normals(0,0,0);
for (Tri_Number=0; Tri_Number<Number_Of_Triangles; Tri_Number++) {
if this vertex exists in this triangle then
triangle_normals+=Triangle[Tri_Number]->Normal;
count=count+1;
}
if (count!=0) {
triangle_normals.x = triangle_normals.x / count;
triangle_normals.y = triangle_normals.y / count;
triangle_normals.z = triangle_normals.z / count;
normalize(triangle_normals);
Vertex[Vertex_Number].normal = triangle_normals;
}
}
Making a directional light is pretty easy, just take the cosine(alpha) of the light vector and the vertex's normal:
dot1=DotProduct(light, v1.normal);
if (dot1<0) dot1=0;
if (dot1>1) dot1=1;
v1.color = dot1*max_intensity;
dot2=DotProduct(light, v2.normal);
if (dot2<0) dot2=0;
if (dot2>1) dot2=1;
v2.color = dot2*max_intensity;
dot3=DotProduct(light, v3.normal);
if (dot3<0) dot3=0;
if (dot3>1) dot3=1;
v3.color = dot3*max_intensity;
Omni light is the same idea:
temp = omni_position - vertex_position;
Normalize(temp);
dot1=DotProduct(v1.normal, temp);
if (dot1<0) dot1=0;
if (dot1>1) dot1=1;
v1.color = dot1*max_intensity;
And do the same with the rest.
It's not 100% accurate?
Yeah, believe it or not, it's still not totally accurate. You are probably thinking right now, haven't I already applied SubPixel accuracy? Yes, sure you have, but what about SubTexel accuracy? Remember that for our pixel to touch the hotlot we had to use the ceil function to round upward the X1 coordinate, the start of the scanline? But what about finding the distance of the current X1 position and the ceil(X1)? We need to prestep the color as well.
d is the distance you need to prestep, should be pretty obvious, IMO.

diStance = ceil(x1) - x1;
color = c1 + diStance*dCdX;
Already done it?
Boy, I'm getting tired of writing this long article, I'll briefly explain how affine-texture-mapping is done. Let's think about what Texture-Mapping is all about, you just grab the texture's coordinates at the beginning of the scanline just like you've done with gouraud filler. Texture coordinates are called U and V, and you increase them with the texture's deltas like you've done in gouraud.
V(1.0)
/|\
|
|
|
|
|
|
o------------------>U(1.0)
That's our texture space, U is the texture's X coordinate and V is the texture's Y coordinate. They are usually scaled to texture resolution. You are supposed to interpolate the U, V of each vertex over the triangle's left edges and draw a texturized scanline between LeftX and RightX. Easy to do, I used here a 256x256 map:
U = LeftU;
V = LeftV;
for (x=x1; x<x2;x++) {
*dest++=texture_map[(int)U + (int)V*256];
U+=dUdX;
V+=dVdX;
}
Just think about it. You interpolate the texture coordinates and then grab the actual texture pixels from the texture map.
One thing I want to note, we are doing affine-linear texture mapping here, which means that it can get perspective distortions and stuff, yuck. Feel that something is missing? Good! Where has the SubTexel accuracy gone to?
x1i = ceil(x1);
x2i = ceil(x2);
distance = ceil(x1) - x1;
U = LeftU + distance*dUdX;
V = LeftV + distance*dVdX;
for (x=x1i; x<x2i;x++) {
*dest++=texture_map[(int)U + (int)V*256];
U+=dUdX;
V+=dVdX;
}
If you understand how texture-mapping works then you should skip to the next chapter.
Still here? OK, let's make a small drawing:
(V=0 for a, b, c, d scanlines, means first row in the texture map)
0
/\
a 1/ \7
b 2/ \14
c 3/ \21
d 4/ \28
A B
We got line A and line B, in line A we see the interpolated U coordinate over the left edge, and in the right line B we see the interpolated U coordinate over the right edge. We need to fill that space between LeftU and RightU with some picture,
dX in line a = 3
dU = 7-1 = 6
dUdX = 6 / 3 = 2
Means that for every pixel we move we grab the pixel after the next pixel in the map.
0
/\
a 1/35\7
b 2/5811\14
c 3/ \21
d 4/ \28
A B
We draw the 3rd pixel from the map and then draw the 5th, let's do it for scanline b as well. Let's say:
dX = 4
dU = 14 - 2 = 12
dUdX = 12/4 = 3
So we draw at:
X=0 map[2]
X=1 map[5]
X=2 map[8]
X=3 map[11]
You must have understood it by now. I don't think it's possible not to understand it, that is if you read everything, but still, feel good with yourself even if you haven't understood it, re-read it after some time when you're not tired.
Perspective correction
So you've done that shitty affine-mapper, cheerz! Now let's get to the real thing, I won't explain any math behind it, I'll just show you how it's done. This method relies on the fact that
U V 1
---, ---, ---
Z Z Z
are linear in screen space while U, V are not. I won't prove it, just know that it works, if you're bored try proving that the line after perspective projection is still the same linear line, or you could use the plane equation. There's lot of info about proving it in the Internet. Or ask on #coders, somebody will help you.
Just calculate new variables, like:
z_a = 1.0 / z1;
z_b = 1.0 / z2;
z_c = 1.0 / z3;
u_a = u1 * z1;
u_b = u2 * z2;
u_c = u3 * z3;
v_a = v1 * z1;
v_b = v2 * z2;
v_c = v3 * z3;
Calculate your dUdX, dVdX, dZdX deltas using those variables. Interpolate normally. Just in your inner loop make some little changes:
for (x=x1; x<x2; x++) {
OnePerZ = 1.0 / Z;
RealU = U*OnePerZ;
RealV = V*OnePerZ;
*dest++=map[RealU + RealV*256];
U+=dUdX;
V+=dVdX;
Z+=dZdX;
}
u
-
z u z
----- = - * - = u
1 z 1
-
z
Same goes for V.
Scanline subdivision
Here's the inner loop from the Perspective Correct Texture Mapper:
for (x=x1; x<x2; x++) {
OnePerZ = 1.0 / Z;
RealU = U*OnePerZ;
RealV = V*OnePerZ;
*dest++=map[RealU + RealV*256];
U+=dUdX;
V+=dVdX;
Z+=dZdX;
}
1 div and 2 muls per pixel, that gotta be sloooow! Seems that correcting every 8th or 16th is enough so why don't we split this scanline to parts? Each part's width is 8 pixels for example. Calculate the correct value in pixel 0th then skip to the 8th pixel, calculate the correct value and interpolate between these two and so on. If your scanline is less than 8 pixels, let's say the size is XX and 0<XX<8, you make the first correction at pixel 0 and skip to pixel XX, apply correction and interpolate.
Apply correction to pixel A, skip to pixel B, apply correction and interpolate between A and B, then skip to C, apply correction and interpolate between B and C and so on.
A B C D
| | | |
|-------|-------|-------|
| | | |
You'd better make your own junk.
#define XRES 320
#define SUB_DIVIDE_SHIFT 4
#define SUB_DIVIDE_SIZE (1<<SUB_DIVIDE_SHIFT)
typedef struct
{
float x, y,z,
u, v;
} PK_Vertex;
float Left_dXdY, Right_dXdY, LeftX, RightX;
float Left_dUdY, LeftU;
float Left_dVdY, LeftV;
float Left_dZdY, LeftZ;
float PK_dudx, PK_dvdx, PK_dzdx;
float PK_dudx_, PK_dvdx_, PK_dzdx_;
unsigned char *dest_ptr,*dest;
#define SUB_PIX(a) (ceil(a)-a)
void DrawSegment(long y1, long y2, unsigned char *textmap);
void swap_ (void * a, void * b);
void Pk_Triangle
(PK_Vertex *v1, PK_Vertex *v2, PK_Vertex *v3, unsigned char *textmap,
unsigned char *where)
{
float u_a, v_a, z_a,
u_b, v_b, z_b,
u_c, v_c, z_c;
if (v1->y > v2->y) swap_(&v1, &v2);
if (v1->y > v3->y) swap_(&v1, &v3);
if (v2->y > v3->y) swap_(&v2, &v3);
long y1i=ceil(v1->y);
long y2i=ceil(v2->y);
long y3i=ceil(v3->y);
if (y1i==y3i) return;
z_a = 1.0 / v1->z;
z_b = 1.0 / v2->z;
z_c = 1.0 / v3->z;
u_a = v1->u * z_a;
u_b = v2->u * z_b;
u_c = v3->u * z_c;
v_a = v1->v * z_a;
v_b = v2->v * z_b;
v_c = v3->v * z_c;
float prestep;
dest_ptr = &where[y1i*XRES];
float dXdY_V1V3=(v3->x - v1->x) / (v3->y - v1->y);
float dXdY_V2V3=(v3->x - v2->x) / (v3->y - v2->y);
float dXdY_V1V2=(v2->x - v1->x) / (v2->y - v1->y);
float dUdY_V1V3=(u_c - u_a) / (v3->y - v1->y);
float dUdY_V2V3=(u_c - u_b) / (v3->y - v2->y);
float dUdY_V1V2=(u_b - u_a) / (v2->y - v1->y);
float dVdY_V1V3=(v_c - v_a) / (v3->y - v1->y);
float dVdY_V2V3=(v_c - v_b) / (v3->y - v2->y);
float dVdY_V1V2=(v_b - v_a) / (v2->y - v1->y);
float dZdY_V1V3=(z_c - z_a) / (v3->y - v1->y);
float dZdY_V2V3=(z_c - z_b) / (v3->y - v2->y);
float dZdY_V1V2=(z_b - z_a) / (v2->y - v1->y);
float denom = ((v3->x - v1->x) * (v2->y - v1->y)
- (v2->x - v1->x) * (v3->y - v1->y));
if (!denom) return;
denom = 1.0f / denom;
PK_dudx=((u_c - u_a) * (v2->y - v1->y) - (u_b - u_a)
* (v3->y - v1->y))*denom;
PK_dvdx=((v_c - v_a) * (v2->y - v1->y) - (v_b - v_a)
* (v3->y - v1->y))*denom;
PK_dzdx=((z_c - z_a) * (v2->y - v1->y) - (z_b - z_a)
* (v3->y - v1->y))*denom;
PK_dudx_=PK_dudx*SUB_DIVIDE_SIZE;
PK_dvdx_=PK_dvdx*SUB_DIVIDE_SIZE;
PK_dzdx_=PK_dzdx*SUB_DIVIDE_SIZE;
bool mid = dXdY_V1V3<dXdY_V1V2;
// if dXdY_V1V3 slope bigger than dXdY_V1V2
// then v2 is at the left side of triangle
if (!mid) {
// v2 at the left side
prestep = SUB_PIX(v1->y);
if (y1i==y2i) {
Left_dUdY = dUdY_V2V3;
Left_dVdY = dVdY_V2V3;
Left_dZdY = dZdY_V2V3;
Left_dXdY = dXdY_V2V3;
Right_dXdY = dXdY_V1V3;
LeftU = u_b + SUB_PIX(v2->y)*Left_dUdY;
LeftV = v_b + SUB_PIX(v2->y)*Left_dVdY;
LeftZ = z_b + SUB_PIX(v2->y)*Left_dZdY;
LeftX = v2->x + SUB_PIX(v2->y)*Left_dXdY;
RightX = v1->x + prestep*Right_dXdY;
DrawSegment(y1i, y3i, textmap);
return;
}
Right_dXdY = dXdY_V1V3;
if (y1i<y2i) {
Left_dUdY = dUdY_V1V2;
Left_dVdY = dVdY_V1V2;
Left_dZdY = dZdY_V1V2;
Left_dXdY = dXdY_V1V2;
LeftU = u_a + prestep*Left_dUdY;
LeftV = v_a + prestep*Left_dVdY;
LeftZ = z_a + prestep*Left_dZdY;
LeftX = v1->x + prestep*Left_dXdY;
RightX = v1->x + prestep*Right_dXdY;
DrawSegment(y1i, y2i, textmap);
}
if (y2i<y3i) {
Left_dXdY = dXdY_V2V3;
Left_dUdY = dUdY_V2V3;
Left_dVdY = dVdY_V2V3;
Left_dZdY = dZdY_V2V3;
LeftU = u_b + SUB_PIX(v2->y)*Left_dUdY;
LeftV = v_b + SUB_PIX(v2->y)*Left_dVdY;
LeftZ = z_b + SUB_PIX(v2->y)*Left_dZdY;
LeftX = v2->x + SUB_PIX(v2->y)*Left_dXdY;
DrawSegment(y2i, y3i, textmap);
}
}
else
if (mid) {
// v2 at the right side
prestep = SUB_PIX(v1->y);
if (y1i==y2i) {
Left_dUdY = dUdY_V1V3;
Left_dVdY = dVdY_V1V3;
Left_dZdY = dZdY_V1V3;
Left_dXdY = dXdY_V1V3;
Right_dXdY = dXdY_V2V3;
LeftU = u_a + prestep*Left_dUdY;
LeftV = v_a + prestep*Left_dVdY;
LeftZ = z_a + prestep*Left_dZdY;
LeftX = v1->x + prestep*Left_dXdY;
RightX = v2->x + SUB_PIX(v2->y)*Right_dXdY;
DrawSegment(y1i, y3i, textmap);
return;
}
Left_dXdY = dXdY_V1V3;
Left_dUdY = dUdY_V1V3;
Left_dVdY = dVdY_V1V3;
Left_dZdY = dZdY_V1V3;
if (y1i<y2i) {
Right_dXdY = dXdY_V1V2;
LeftU = u_a + prestep*Left_dUdY;
LeftV = v_a + prestep*Left_dVdY;
LeftZ = z_a + prestep*Left_dZdY;
LeftX = v1->x + prestep*Left_dXdY;
RightX = v1->x + prestep*Right_dXdY;
DrawSegment(y1i, y2i, textmap);
}
if (y2i<y3i) {
Right_dXdY = dXdY_V2V3;
RightX = v2->x + SUB_PIX(v2->y)*Right_dXdY;
DrawSegment(y2i, y3i, textmap);
}
}
}
// ecx = x2-x1
// eax = u1 16:16
// edx = v1 16:16
// esi = texturemap
// edi = destination
#pragma aux affine_tline=\
"push ebp"\
"test ecx,ecx"\
"jle @eend"\
"mov ebp,ecx"\
"add edi,ebp"\
"xor ebp,-1"\
"inc ebp"\
"@inner:"\
"mov ebx,eax"\
"mov ecx,edx"\
"and ebx,0xff0000"\
"and ecx,0xff0000"\
"shr ebx,16"\
"shr ecx,8"\
"add ecx,ebx"\
"mov bl,[esi+ecx]"\
"mov [edi+ebp],bl"\
"add eax,[DU]"\
"add edx,[DV]"\
"inc ebp"\
"jnz @inner"\
"@eend:"\
"pop ebp"\
parm [ecx] [eax] [edx] [esi] [edi] modify [eax ebx ecx edx edi];
// dx u v src dst
inline void DrawSegment(long y1, long y2, unsigned char *textmap)
{
float u, v, z, Z;
long du, dv, width;
long U, V, U1, V1, U2, V2;
long x1, x2, y, x;
for (y=y1;y<y2;y++) {
x1 = ceil(LeftX);
x2 = ceil(RightX);
dest = dest_ptr+x1;
u = LeftU + SUB_PIX(LeftX)*PK_dudx;
v = LeftV + SUB_PIX(LeftX)*PK_dvdx;
z = LeftZ + SUB_PIX(LeftX)*PK_dzdx;
Z = 65536.0 / z;
U2 = u*Z;
V2 = v*Z;
width = x2 - x1;
while (width>=SUB_DIVIDE_SIZE) {
u+=PK_dudx_;
v+=PK_dvdx_;
z+=PK_dzdx_;
U1 = U2;
V1 = V2;
Z = 65536 / z;
U2 = u*Z;
V2 = v*Z;
du = (U2 - U1) >> SUB_DIVIDE_SHIFT;
dv = (V2 - V1) >> SUB_DIVIDE_SHIFT;
U=U1;
V=V1;
x = SUB_DIVIDE_SIZE;
while (x--) {
*dest++=textmap[( (U&0xFF0000)>>16 )
+ ( (V & 0xFF0000)>>8 )];
U+=du;
V+=dv;
}
width-=SUB_DIVIDE_SIZE;
}
if (width>0) {
U1 = U2;
V1 = V2;
u+=(PK_dudx*width);
v+=(PK_dvdx*width);
z+=(PK_dzdx*width);
Z = 65536.0 / z;
U2 = u*Z;
V2 = v*Z;
du = (U2 - U1) / width;
dv = (V2 - V1) / width;
U=U1;
V=V1;
while (width--) {
*dest++=textmap[( U>>16 )
+ ( (V & 0xFF0000)>>8 )];
U+=du;
V+=dv;
}
}
LeftU+=Left_dUdY;
LeftV+=Left_dVdY;
LeftZ+=Left_dZdY;
LeftX+=Left_dXdY;
RightX+=Right_dXdY;
dest_ptr+=XRES;
}
}
#pragma aux swap_ = \
"mov ebx, [eax]"\
"mov ecx, [edx]"\
"mov [edx], ebx"\
"mov [eax], ecx"\
parm [eax] [edx] \
modify [ebx ecx];
What is zbuffer?
Zbuffer is a buffer the size of the screen which represents the depth value of each pixel. How to do it? Just interpolate your Z over the left edges of the triangle.
float zbuffer[320*200]; // will work fine
for (x=x1;x<x2;x++) {
if (z<zbuffer[x+y*320]) {
plot the pixel
zbuffer[x+y*320]=z;
}
z+=dZdX;
}
That will work only if the closer Z is the smaller one, otherwise change the direction to ">" instead of "<".
What is wbuffer?
Wbuffer is just a 1/z buffer, remember that theory that 1/z is linear in screen space? You should interpolate 1/z rather than z 'cause that will be perspective corrected as well.
for (x=x1;x<x2;x++) {
if (z>zbuffer[x+y*320]) {
plot the pixel
zbuffer[x+y*320]=z;
}
z+=dZdX;
}
How do I feel?
Does anybody really care how I feel? I'm exhausted after writing this long article. I really hope that this article helped somebody. If it has please email me and tell me that I haven't written it for nothing. It should cover all the needed basics. Now you, the reader, should be able to build some kick-ass engine, understand things better, make a better world without wars, take over your toiled again, rape your dog, the choices are infinite.
Greets
I'll take this opportunity to thank my mental teacher Kalms, he knows why. Greetz in random order:
frenzy, kalms, sarwaz, salami, dvb, tnse^1999, altair, absent, macaw, greco, action, adept, submissive, kombat, sunday, katrikan, silvatar, tomh, mirek, vastator, nick-s, mrz, adok, velocity, v-man, coaxcable, sol_hsa, cube, yoyo, borzom, parody, graffik, attack, matja, vec, middy, silent breed, kutepixel, xerxes, c-bus, mali, midnight, scriptum, void, psychic sympony, ex, rodex, sagacity, raiden, gday, twobear, firedge, ravian, wog, xls, faktorii, shock, asm[exe], [ad]turbo, darkman, lnx, zoo-b, bacter, trashey, cycat, odin, radium, idiotboy.
Hot greetz to all Winter in July, Mistery, ZeroDefects members!!!!!
EFnet: #coders, #math
IRCNet: #pixel, #coders and #3dcoders of course