Polygonizing Of Implicit Surfaces
Black
What are iso surfaces?
Well, iso surfaces are representation of volume data, but I will refer to them as density fields, since that is a more appropriate term. Here we will speak of only one type of surface representation and that are meta balls; a meta ball is defined with the equation 1/r^2. If you print the graph for y=1/x^2 for x [0..n], n being positive infinity (or 100 will do), you will get the projection of the density field. You can see that the density of the meta ball is very big on the center, and decreasing with the radius. If you add 1/r^2 projection to 2d space you will get an environment like a picture map, which should be added on the top of another. If we draw only some unique value that we set, we will get a circle for one meta ball, two circles for two if the centers are far away or one big one if the centers overlap. If the distance between the centers is small you will get two circles morphing into one. This is the whole trick to polygonization of the density field. All you need to do is to apply 1/r^2 to a 3 dimensional grid, and polygonize the density field with an algorithm that is called marching cubes.
Ok, I will start here, presuming that you have at least some basic knowledge about polygonizing implicit surfaces. The work that you will be able to see here is basic theory and I will make stuff up as we go along.
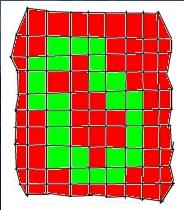
Assuming you polygonized these things before, you could do it in three basic ways regarding cube checking. The first way would be to check all cubes. Figure 1 (2d):

As you see by the red colour that method is very wasteful and so the algorithm of polygonizing here is quite a bit slow. Then there came another method: using bounding boxes. That increased the speed a lot, so around 20-30 fps would be a standard even on a 32x32x32 grid. Figure 2:
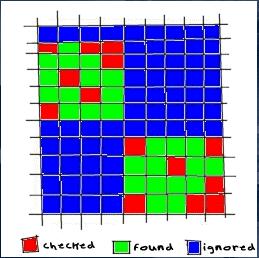
With the structures I used that was a bit wasteful, since I calculated 1/r^2 eight times per vertex sometimes! (Thanks, pan, for pointing that out.)
But still the boundary box thing is a very good idea but the thing can go faster and/or more usable (less checks). Let's say if we rendered a sphere on a 32x32x32 iso surface grid in the first way (check all) we would have 32^3 checks for the iso surface but with the bounding box system we would only have 10^3 (if r==5), but with the third system that I will explain here, we can get a ratio of ranging to about 100% of the iso surface + the radius of the iso surface in grid cells * number of iso surface centers. By the number of iso surface centers I mean just a point that is contained in the iso surface because the previous definition does not agree with the torus (actually it agrees, but toruses have an inner and an outer radius, so setting the point in between reduces iso surface checking). Okay, our first figure in the algorithm.
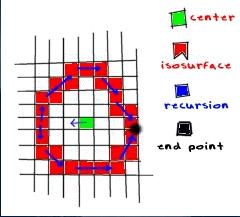
We start our search in the middle of the iso surface and go left down the x axis. For each block we call a recursive function that we will write a bit later on, just for the hell of it. Let's say the function returns 0 in case the box is in/out of the iso surface and 1 if it lies on the iso surface.
int search_center(int xbox, int ybox, int zbox)
// we pass the function the center of the iso surface (the box's x,y,z)
{
for (int x=xbox; x==0; x--) // loop down the x axis
if (polygonize_rec(x,ybox,zbox)) return 1; // all done
// there is no need to check all other cubes.
return 0; // this happens only if the left edge of the iso surface
// is not in the boundaries of the 3d grid.
}
We haven't even started the thing to the full potential and we already have one leak. What if the iso surface doesn't all fit in the gridcells? Well if you want a partial rendering then just use the above procedure, only loop in the other way or some other axis, or just increase the grid item array. For the rendering of metaballs, i.e. blobs, bloby objects, meta spheres, this routine does just fine, if you of course limit the positions of blobs, so that they always fit into the grid array. Another trick when rendering large iso surfaces: decrease the iso value for a bit if the above function doesn't deliver the right information.
Another example
Let's say vertex 0 and 3 are below the iso surface. cubeindex will then be 0000 1001 == 9. The 9th entry in the egdeTable is 905hex == 1001 0000 0101 which means edge 11,8,2, and 0 are cut and so we work out the vertices of the intersection of the iso surface with those edges. Next, 9 in the triTable is 0, 11, 2, 8, 11, 0. This corresponds to two triangular facets, one between the intersection of edge 0, 11, and 2. The other between the intersections along edges 8 11 and 0.
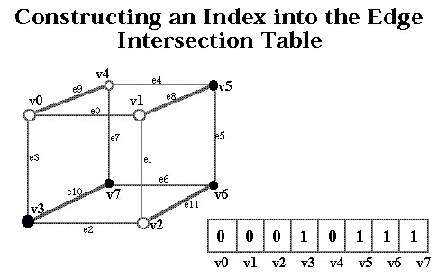
As you notice v3, v5, v6 and v7 are below the iso level, thus creating the combination 00010111.
That's about it. Now let's look at some potential with using bounding boxes and the potential of using recursive polygonizing. For example, if you look at intros nowadays, let's say "Kill the Clone" from Fudge, you see implicit surfaces in there, used in the most original way I saw them being used ever since first demos with blobs occurred. The effect in "Kill the Clone" is very easy to fake now that you read this doc. As a metaball is defined with 1/r^2, you get very high "density" values in the middle of the blob, but let's say we don't clear the grid? As the 1/r^2 adds up per frame the density gets closer to positive infinity, but we don't want that, so let's say we substract 1.0 from the "density" field per frame, and add the blobs on the next position. You get a trail following the blob just like in "Kill the Clone" from Fudge. Ok, not exactly true, might want to substract a smaller number, for example 0.02 or something... it should make the trail more long. This is of course only possible with recursive. If you use bbox, then you should put let's say for example 6 blobs in a trail, with decreasing size toward the ending blob. That should do the trick, but the results might look a bit less satisfactory.
As this was basic and plain theory, I might as well test it now...
Black^Twilight^SpinningKids