3D Clipping
Howdy people, this article is about clipping against frustum planes, I'll explain how to perform full 3d-clipping.
Now it's time to get busy, you probably ask yourself why the hell you should clip polygons when you can just perform 2d-clipping inside the rasterizer. Well, it was tested and proven that finding the intersection points in clipping is faster than 2d-clipping in the rasterizer.
Only a few words before we continue: There is a 4d coordinate system called homogenious coordinate system. It's applied when using 4x4 matrices. A vector will be represtend as [x,y,z,w] instead of [x,y,z,1]. I don't know much about it, but I heard that it makes clipping faster, so it would be a good idea to get some information on it.
Another thing: It is a good idea not to perform all clipping in 3d, since checking whether the point is in the positive or in the negative area of the plane is very expensive and it is highly suggested not to do so (on the other hand, if you do clipping in 3d you will get very accurate results). You should clip against z-near and z-far planes in 3d and after that perform 2d clipping by finding the intersection points with screen boundaries and drawing all polygons.
There is another method if you don't want to mess with homogen' coords. If you streach your frustum pyramid to 90 degrees, you can check:
if X<-Z then it needs to be clipped against the left plane, if X>Z then it needs to be clipped against the right plane, if Y<-Z then it needs to be clipped against the up plane, and if Y>Z then it needs to be clipped against the bottom plane.
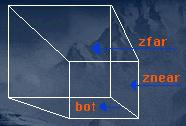
Now you probably ask yourself what frustum is. Frustum is a view cone, in other words it is just a 3d pyramid that can be made out of six planes:
Left, Right, Top, Bottom, Z-Near and Z-Far.
I didn't want to confuse you, that's why I didn't put arrows on all planes.

It's time to get into some vector math: A plane can be made out of 3 points.
We'll do all examples in 320x200 resolution. Our center is at (0, 0, 0) and our screen boundaries are at:
Top left edge (-160, +100, 0)
Top right edge (+160, +100, 0)
Bottom left edge (-160, -100, 0)
Bottom right edge (+160, -100, 0)
OK, let's form some planes (all examples are done with vectors):
Left Plane
We have top_left and bottom_left edges, now there's a tiny problem: Where the fuck is the 3rd point?? The 3rd point is called COP (Center Of Projection) and is located at (0, 0, -projection_distance), while projection_distance is the distance from your eye to the projection plane (the 2d screen).
Now that we're done with that shit, let's make that damn plane:
a = COP (0, 0, -d)
b = top_left (-160, 100, 0)
c = bottom_left (-160, -100, 0)
v1 = b - a = (-160, 100, d)
v2 = c - a = (-160, -100, d)
normal = v1 x v2
Finally normalize it (who needs this huge magnitude anyway?). Btw, you do the same thing when calculating face_normals.
Notice: All plane normals must point inside the frustum!!
Since all the planes go through the origin, the distance to the origin is 0.
Btw, unless you calculate the cross_production of the vectors on the paper, you can't know where the resulting vector will point to, so if you get some fuck up or something, it's usually 'coz the direction of the resulting vector doesn't point into the frustum.
Right Plane
a = COP (0, 0, -d)
b = top_right (160, 100, 0)
c = bottom_right (160, -100, 0)
v1 = b - a = (160, 100, d)
v2 = c - a = (160, -100, d)
normal = v2 x v1
Normalize it.
The distance to origin is always zero. Btw: Try playing with the distances so you understand it better.
You have probably noticed that it's v2 x v1 instead of v1 x v2. If you do v1 x v2 then the right plane normal will point out-of-frustum.
Top Plane
a = COP (0, 0, -d)
b = top_right ( 160, 100, 0)
c = top_left (-160, 100, 0)
v1 = b - a = ( 160, 100, d)
v2 = c - a = (-160, 100, d)
normal = v1 x v2
Normalize it. Distance to origin is zero.
Bottom Plane
a = COP (0, 0, -d)
b = bot_left (-160, -100, 0)
c = bot_right ( 160, -100, 0)
v1 = b - a = (-160, -100, d)
v2 = c - a = ( 160, -100, d)
normal = v1 x v2
Normalize it. Distance to origin is zero.
There are two more planes left, znear and zfar planes. For znear I use (0,0,1) as its normal and distance = -10, which means 10 units behind projection plane. Try changing the distance to 150 or so.
For the zfar plane I use (0,0,-1). You should adjust the distance for each scene, try using something like distance = -2000 at the beginning, just experiment with it.
Now that we have our frustum planes, you need to clip a triangle against each of those planes. As you know that triangle has three sections, each of which can be described as a line.
Finding the distance from a point to a plane can be done like this:
dot - dot product
distance = plane_normal dot point.
You also need to know the linear interpolation formula:
I - the interpolated value
A - starting point
B - ending point
t - interpolation factor, whose value is 0..1
I = A + t(B-A)
Let's do a small example. There is a line which has a starting X=0 and ending X=10 and also a starting color = 10 and ending color = 60.
A->x = 0; B->x = 10;
If we want to find the color at the middle of this line then t = 0.5. We can also calculate the t:
I->x = A->x + t(B->x - A->x)
5 = 0 + t(10 - 0)
5 = 10t
t = 5/10 = 0.5 (:
For calculating the color or any value you want at X=5 you just do:
I->color = A->color + t(B->color - A->color)
Or more general formula -> I->value = A->value + t(B->value - A->value)
After knowing that we can calculate the intersected points with the plane, I'll show you later how to perform line-by-line clipping.
A - starting point of the line
B - ending point of the line
distance1 = point_2_plane_distance(A, plane);
distance2 = point_2_plane_distance(B, plane);
while point_2_plane_distance(point, plane) = (point dot plane) -plane.distance
t = distance1 / (distance1 - distance2)
And finding the intersected point, which is done by linear interpolation:
I->x = A->x + t(B->x - A->x)
I->y = A->y + t(B->y - A->y)
I->z = A->z + t(B->z - A->z)
I->u = A->u + t(B->u - A->u)
I->v = A->v + t(B->v - A->v)
And any value you want.
Line-by-line clipping
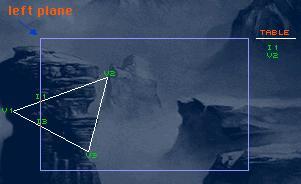
Here's a picture of an un-clipped polygon:
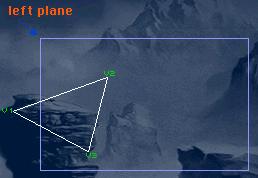
I'll give an example only against the left plane. As you can see there's one point v1 in the backside of the plane and the two others points on the positive side of the plane, which means that 1 point is invisible and 2 are visible.
I'll mark the visible lines with white color, and with the orange color the intersected points.
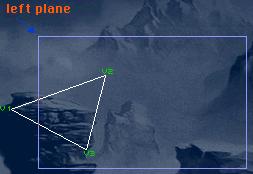
Btw: After clipping you usually won't get a triangle but a quad or some n-gon.
There are only 2 intersected points, I1 and I3. There is a table on the right side in which I'll list all the vertices I need to draw. So let's start:
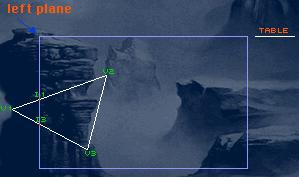
The line v1 to v2 leaves the backside of the plane, so we list the intersected point and v2 in the table.
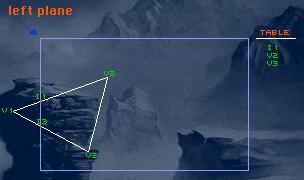
The line from v2 to v3 is fully visible, so you just put v3 into the table.
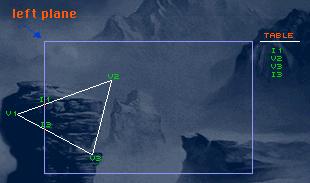
The line from v3 to v1 tries to enter the invisble area, so you just put the intersected point I3 in the table.
If you still haven't understood the algo, it is: if the line leaves the invisible area then put the intersected point and the ending point of the line in the array. If the line tries to enter the invisble side then you put only the intersected point in the array.
You probably thinking that you should code a n-gon. That could be nice but for all the other lazy arses out there you can just do:
nout - number of points resulted after performing clipping
for (i=0;i<nout-2;i++) triangle(table[0], table[i+1], table[i+2]);
Here's an example:
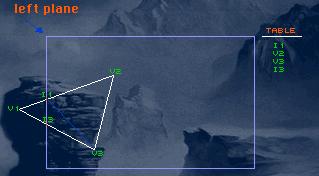
I hope you know that you have to do all that before perspective projection 'cause you can't perspective project with z=0, that's one of the reasons for clipping.
Some optimization tips
You could generate out-codes for the object to see against what planes to clip, you could also set out-codes for every vertice to make the line-by-line clipping a little faster.
For the start just generate a boundary box for each object, it can be made out of 8 vertices, just find xmin, ymin, zmin and xmax, ymax, zmax and make a box out of that.
After you have your box just apply all transformations on the box in the same way as you apply on your object and check only 8 vertices against frustum planes, so you won't do any more than you need.
There isn't much to write about it. Bounding spheres are also cute, just find the sphere centre and sphere radius, and tada, transform spheres centre like you transform the object and do some checks with distance from centre of sphere to the plane and its radius. It's not that hard, try doing it by yourself on paper.
Greetz fly to
Kombat, Kalms, xls, Salami, Adok, Greco, dvb, Rodex, Adept, Ex, Borzom, Cycat, Trashey, Biomas, Yoyo, Sosay, Radium, Matja, Cube, asm[exe], Civax, tnse^98, Submissive, Octan, Zippy, Voltaire, Phred, Nick-S, mrz, macaw, lord^crc, GooRoo, Sagacity, Sarix, Armitage, Jeffry Lim, DJ-Gfunk, Octan, Velocity, Javier Arevalo, Smallbrain, Tanis, Parody, idiotboy, gyr, Silent Breed, Barog, Shock, Yaron, Crest, MAD, Midnight, Silvatar, Diffuse, Tetris, Mirek, Buffer, Krembo, Vampire_X, Vor, Altair, frenzy, CoaXCable, MRI, Muaddib, Buran, GDay, oyd, Absent, icepick, Idol, Sarwaz...
Immortals, Quasars, Ivory, Flood, $een, Trauma, Moon Hunters, Nothing, Quad, TBL, Yoe, Pulse, Hugi Team, party orginizers all over the world and all the others that keep the demo scene alive.
Salami and Kalms deserve another greet. :)
Double special thanks go to:
Kombat - For explaining how 3ds does all the keyframing, some more coding help and also for being a k00l dude.
Kalms - For all the coding help, technical and moral support.
Adept - For messing with kochanek bartel splines and releasing your hack on them. :-)
Salami - Where would I be now without your support in all ways, keep up the good work mate.
Submissive - For his gr8 tuts.
If I forgot you, flame me and I write your name. The chances that I haven't forgot you are high though, it's the longest greet list I've ever written. (: