On-The-Fly Continuous Level Of Detail Generation For Polygonal Meshes
Motivation
The quality of real-time 3d graphics rendering is at least partially proportional to the geometric detail of the meshes involved. If powerful object occlusion culling algorithms can be used, what is left is the geometry of the visible objects. The idea behind using different level of details (LODs) for individual meshes or models is that frame buffer resolution is usually fixed and thus, at greater distances the objects need less geometric resolution than near ones because they cover less frame buffer area.
Until recently, the way to use LOD capabilities in interactive 3d programs, was to have several copies of each objects prestored in the memory at different LODs. This technique has several drawbacks. Firstly, the memory consumption can be huge in normal situations or prohibitive in large-scale models. The memory consumption also creates related problems such as decreased cache utilization. Secondly, only a (small) set of precomputed LODs can be used, unlike the (semi-)continuous LOD presented here. Thirdly, it is usable in static (non-deforming) objects only. For deformable objects, on-the-fly LOD generation is needed as presented below.
Algorithms
Different approaches can be taken to generating models at different LODs. A global approach to the problem is to optimize the model at a given LOD to match the highest-detail model as closely as possible. This approach is not a reasonable alternative for real-time applications where computational performance is vital. Iterative approaches can still be optimal, if a given LOD model is matched to the model at a LOD from previous iteration.
Iterative, local approaches are best viewed as operators on the mesh geometry. That is, each successive step of the LOD decrease/increase process for instance removes (collapses) an edge from the mesh or inserts two vertices into the mesh, as is done here. The rest of the section refers to this basic operation: collapsing an edge into a vertex, thus, two vertices defining an edge are replaced by a single new one.
The algorithm is a simple iterative process: at each iteration, an edge is removed from the mesh, thus providing a smooth ("continuous") level-of-detail control over the model. The edge chosen for removal at each stage is the one that contributes least to the difference between the current LOD and the LOD from previous iteration. The measure is defined as an energy function, which is a function of the two points connecting the edge. The rationality behind is that the visual and numerical error arises when the two points of the edge are moved away from the model's surface.
The energy function is taken from: Sebastien Loisel: Vertex Collapse Using a Quadratic Error Metric and is repeated here for convenience. We define the "error" of a vertex to be the sum of square distances to the planes of polygons it belongs to, multiplied by the area of those polygons. This measure has several benefits, first of them being that each step aims at preserving the volume of the model, though of course globally (across several iterations) this is not the case. Secondly, the area of the polygons that are affected by the collapsed edge is taken into account, and thus small, visually less important features of the model are likely to disappear first.
Thus, after some simplifications performed on the formula the error (energy) function for a vertex is defined as:
The vector x is a 4d homogenous representation of the given vertex and the vector Q is a 4d vector representing the 4 coefficients of the plane's equation. The summation is over the set of polygons P that share the given vertex. Now, to obtain the error function for an edge, we sum the energy functions of the two vertices that define that edge. We perform minimization on the error function to find an optimal point, and at each iteration of the LOD algorithm, we choose an edge with the minimum error.
Therefore, for each edge we set the gradient of the error function to zero and solve the system of simultaneous equations, thus effectively choosing an optimal edge at each step:
Implementation and results
The algorithm assumes that, at each step, the simultaneous equations are solved at each step. This is actually not needed, as we can store the results in the memory (one vertex and the energy value per edge), if memory space is not a constraint. With a topological data structure such as the winged-edge structure, adjacency and membership relationships can be computed easily in constant time. Thus, each iteration of the LOD algorithm can be performed in logarithmic time and linear space or linear time and constant space.
There are further optimizations possible if the objects are known to be non-deforming or do not deform radically during the interactive rendering process. Namely, the sequence of edge collapses can be pre-stored and save in very little space (typically around few bytes per vertex). Then, at each step, we simply traverse the list in constant time. The variant which computes the optimal edge collapses on-the-fly is not much slower, but we don't have to use (somewhat) cumbersome winged-edge list during the actual rendering.
Special care has to be taken in case of singularities of the matrix forming the simultaneous equations. This can easily arise when the triangles sharing the vertices are coplanar, for instance. My method is to use the Singular Value Decomposition of the matrix, with which singularity check is trivial and in case of singularity, it provides one with the solution space automatically. Then, the least-squares solution nearest the original edge is chosen since then, the resulting new vertex is closest to the two original vertices.
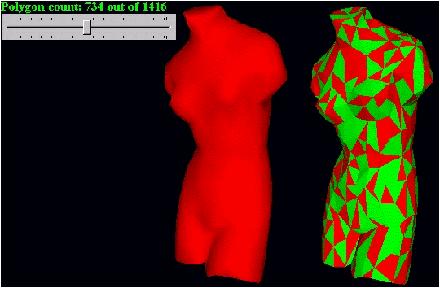
An interactive OpenGL implementation is available, which allows to visualise the effect of decreasing and increasing level of detail on a moderately complex object (Venus de Milo). The program requires Windows 95/98/NT as well as the Microsoft OpenGL dynamic link libraries.
After the implementation, it was pointed out to me by several people that the original algorithm which Loisel's paper refers to is Michael Garland et al's paper from SIGGRAPH'97 proceedings. The paper is indeed a very nice explanation as well, but it misses a couple of details and the implementation runs far from real-time even on the SGI super-workstation.
Download: Continuous LOD demonstrator in OpenGL, 205 kB
The following is one screenshot from the program: